Το θεώρημα του σχήματος του Holland

Το θεώρημα του Holland για το σχήμα, το οποίο ονομάζεται επίσης θεμελιώδες θεώρημα των γενετικών αλγορίθμων, είναι μια ανισότητα που προκύπτει από την χονδροειδή διαμόρφωση μιας εξίσωσης για την εξελικτική δυναμική. Το θεώρημα σχήματος λέει ότι τα σύντομα, χαμηλής τάξης σχήματα με καταλληλότητα άνω του μέσου όρου αυξάνονται εκθετικά σε συχνότητα στις διαδοχικές γενιές. Το θεώρημα προτάθηκε από τον John Holland τη δεκαετία του 1970. Αρχικά θεωρήθηκε ευρέως ότι αποτελεί τη βάση για τις εξηγήσεις της ισχύος των γενετικών αλγορίθμων. Ωστόσο, αυτή η ερμηνεία των συνεπειών του επικρίθηκε σε διάφορες δημοσιεύσεις που εξετάστηκαν στο , όπου το Θεώρημα Σχήματος αποδεικνύεται ότι αποτελεί ειδική περίπτωση της εξίσωσης Price με τη συνάρτηση δείκτη σχήματος ως μακροσκοπική μέτρηση.

Ένα σχήμα είναι ένα πρότυπο που προσδιορίζει ένα υποσύνολο συμβολοσειρών με ομοιότητες σε ορισμένες θέσεις συμβολοσειρών. Τα σχήματα αποτελούν ειδική περίπτωση των κυλινδρικών συνόλων και, ως εκ τούτου, σχηματίζουν έναν τοπολογικό χώρο.

Περιγραφή

Θεωρήστε δυαδικές συμβολοσειρές μήκους 6. Το σχήμα 1*10*1 περιγράφει το σύνολο όλων των συμβολοσειρών μήκους 6 με 1 στις θέσεις 1, 3 και 6 και 0 στη θέση 4. Το * είναι ένα σύμβολο μπαλαντέρ, που σημαίνει ότι οι θέσεις 2 και 5 μπορούν να έχουν τιμή είτε 1 είτε 0. Η σειρά ενός σχήματος o ( H ) {\displaystyle o(H)} $o(H)$ ορίζεται ως ο αριθμός των σταθερών θέσεων στο πρότυπο, ενώ το μήκος ορισμού δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ είναι η απόσταση μεταξύ της πρώτης και της τελευταίας συγκεκριμένης θέσης. Η τάξη του 1*10*1 είναι 4 και το μήκος ορισμού του είναι 5. Η καταλληλότητα ενός σχήματος είναι η μέση καταλληλότητα όλων των συμβολοσειρών που ταιριάζουν στο σχήμα. Η καταλληλότητα μιας συμβολοσειράς είναι ένα μέτρο της αξίας της κωδικοποιημένης λύσης του προβλήματος, όπως υπολογίζεται από μια ειδική για το πρόβλημα συνάρτηση αξιολόγησης. Χρησιμοποιώντας τις καθιερωμένες μεθόδους και τους γενετικούς τελεστές των γενετικών αλγορίθμων, το θεώρημα του σχήματος δηλώνει ότι τα σύντομα σχήματα χαμηλής τάξης με καταλληλότητα πάνω από το μέσο όρο αυξάνονται εκθετικά στις διαδοχικές γενιές. Εκφράζεται ως εξίσωση:

E ( m ( H , t + 1 ) ) ≥ m ( H , t ) f ( H ) a t [ 1 - p ] . {\displaystyle \operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p]. } $\operatorname {E} (m(H,t+1))\geq {m(H,t)f(H) \over a_{t}}[1-p].$

Εδώ m ( H , t ) {\displaystyle m(H,t)} $m(H,t)$ είναι ο αριθμός των συμβολοσειρών που ανήκουν στο σχήμα H {\displaystyle H} $H$ στη γενιά t {\displaystyle t} $t$ , f ( H ) {\displaystyle f(H)} $f(H)$ είναι η παρατηρούμενη μέση καταλληλότητα του σχήματος H {\displaystyle H} $H$ και a t {\displaystyle a_{t}} $a_{t}$ είναι η παρατηρούμενη μέση καταλληλότητα στη γενιά t {\displaystyle t} $t$ . Η πιθανότητα διάσπασης p {\displaystyle p} $p$ είναι η πιθανότητα η διασταύρωση ή η μετάλλαξη να καταστρέψει το σχήμα H {\displaystyle H} $H$ . Μπορεί να εκφραστεί ως εξής:

p = δ ( H ) l - 1 p c + o ( H ) p m {\displaystyle p={\delta (H) \over l-1}p_{c}+o(H)p_{m}} $p={\delta (H) \over l-1}p_{c}+o(H)p_{m}$

όπου o ( H ) {\displaystyle o(H)} $o(H)$ είναι η σειρά του σχήματος, l {\displaystyle l} $l$ είναι το μήκος του κώδικα, p m {\displaystyle p_{m}} $p_{m}$ είναι η πιθανότητα μετάλλαξης και p c {\displaystyle p_{c}} $p_{c}$ είναι η πιθανότητα διασταύρωσης. Έτσι, ένα σχήμα με μικρότερο μήκος ορισμού δ ( H ) {\displaystyle \delta (H)} $\delta (H)$ είναι λιγότερο πιθανό να διαταραχθεί.
Ένα συχνά παρεξηγημένο σημείο είναι γιατί το Θεώρημα Σχήματος είναι ανισότητα και όχι ισότητα. Η απάντηση είναι στην πραγματικότητα απλή: το Θεώρημα αμελεί τη μικρή, αλλά μη μηδενική, πιθανότητα μια συμβολοσειρά που ανήκει στο σχήμα H {\displaystyle H} $H$ να δημιουργηθεί "από το μηδέν" με μετάλλαξη μιας μεμονωμένης συμβολοσειράς (ή ανασυνδυασμό δύο συμβολοσειρών) που δεν ανήκε στο H {\displaystyle H} $H$ στην προηγούμενη γενιά.

Περιορισμός

Το θεώρημα του σχήματος ισχύει υπό την υπόθεση ενός γενετικού αλγορίθμου που διατηρεί έναν απείρως μεγάλο πληθυσμό, αλλά δεν μεταφέρεται πάντα στην (πεπερασμένη) πράξη: λόγω του σφάλματος δειγματοληψίας στον αρχικό πληθυσμό, οι γενετικοί αλγόριθμοι μπορεί να συγκλίνουν σε σχήματα που δεν έχουν κανένα επιλεκτικό πλεονέκτημα. Αυτό συμβαίνει ιδίως στην πολυτροπική βελτιστοποίηση, όπου μια συνάρτηση μπορεί να έχει πολλαπλές κορυφές: ο πληθυσμός μπορεί να παρασυρθεί ώστε να προτιμά μία από τις κορυφές, αγνοώντας τις άλλες.

Ο λόγος για τον οποίο το Θεώρημα του Σχήματος δεν μπορεί να εξηγήσει την ισχύ των γενετικών αλγορίθμων είναι ότι ισχύει για όλες τις περιπτώσεις προβλημάτων και δεν μπορεί να κάνει διάκριση μεταξύ προβλημάτων στα οποία οι γενετικοί αλγόριθμοι αποδίδουν ελάχιστα και προβλημάτων στα οποία οι γενετικοί αλγόριθμοι αποδίδουν καλά.

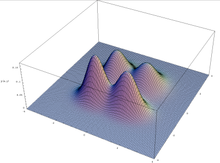
Γραφική παράσταση μιας πολυτροπικής συνάρτησης σε δύο μεταβλητές.

Ερωτήσεις και απαντήσεις

Ερ: Τι είναι το θεώρημα του σχήματος του Holland;

A: Το θεώρημα σχήματος του Holland είναι ένα θεώρημα σχετικά με τους γενετικούς αλγορίθμους που λέει ότι τα άτομα με καταλληλότητα υψηλότερη από το μέσο όρο είναι πιο πιθανό να επικρατήσουν.

Ε: Ποιος πρότεινε το θεώρημα του Holland και πότε;

Α: Ο John Holland πρότεινε το θεώρημα του σχήματος του Holland τη δεκαετία του 1970.

Ερ: Τι είναι το σχήμα στο πλαίσιο των γενετικών αλγορίθμων;

Α: Στο πλαίσιο των γενετικών αλγορίθμων, ένα σχήμα είναι ένα πρότυπο που προσδιορίζει ένα υποσύνολο συμβολοσειρών με ομοιότητες σε ορισμένες θέσεις συμβολοσειρών.

Ερ: Ποια είναι η ερμηνεία του θεωρήματος σχήματος του Holland που χρησιμοποιήθηκε ως βάση για τις εξηγήσεις της ισχύος των γενετικών αλγορίθμων;

A: Η ερμηνεία του θεωρήματος του σχήματος του Holland που χρησιμοποιήθηκε ως θεμέλιο για τις εξηγήσεις της ισχύος των γενετικών αλγορίθμων είναι ότι τα άτομα με φυσική κατάσταση υψηλότερη του μέσου όρου έχουν περισσότερες πιθανότητες να επικρατήσουν.

Ερ: Τι έχει δείξει η κριτική του θεωρήματος του σχήματος του Holland;

Α: Η κριτική στο θεώρημα του Holland για το σχήμα έδειξε ότι είναι μια ειδική περίπτωση της εξίσωσης Price με τη συνάρτηση δείκτη σχήματος ως μακροσκοπική μέτρηση.

Ερ: Ποια είναι μια ειδική περίπτωση των κυλινδρικών συνόλων;

Α: Τα σχήματα αποτελούν ειδική περίπτωση των κυλινδρικών συνόλων.

Ερ: Τι είδους χώρο σχηματίζουν τα σχήματα;

Α: Τα σχήματα σχηματίζουν έναν τοπολογικό χώρο.