Γραμμική παλινδρόμηση
Η γραμμική παλινδρόμηση είναι ένας τρόπος εξήγησης της σχέσης μεταξύ μιας εξαρτημένης μεταβλητής και μιας ή περισσότερων επεξηγηματικών μεταβλητών με τη χρήση μιας ευθείας γραμμής. Αποτελεί ειδική περίπτωση της ανάλυσης παλινδρόμησης.
Η γραμμική παλινδρόμηση ήταν ο πρώτος τύπος ανάλυσης παλινδρόμησης που μελετήθηκε αυστηρά. Αυτό οφείλεται στο γεγονός ότι τα μοντέλα που εξαρτώνται γραμμικά από τις άγνωστες παραμέτρους τους είναι ευκολότερο να προσαρμοστούν από τα μοντέλα που σχετίζονται μη γραμμικά με τις παραμέτρους τους. Επιπλέον, οι στατιστικές ιδιότητες των εκτιμητών που προκύπτουν είναι ευκολότερο να προσδιοριστούν.
Η γραμμική παλινδρόμηση έχει πολλές πρακτικές χρήσεις. Οι περισσότερες εφαρμογές εμπίπτουν σε μία από τις ακόλουθες δύο μεγάλες κατηγορίες:
- Η γραμμική παλινδρόμηση μπορεί να χρησιμοποιηθεί για την προσαρμογή ενός προγνωστικού μοντέλου σε ένα σύνολο παρατηρούμενων τιμών (δεδομένων). Αυτό είναι χρήσιμο, εάν ο στόχος είναι η πρόβλεψη, ή η πρόβλεψη, ή η μείωση. Μετά την ανάπτυξη ενός τέτοιου μοντέλου, εάν στη συνέχεια δοθεί μια πρόσθετη τιμή του Χ χωρίς τη συνοδευτική τιμή του y, το προσαρμοσμένο μοντέλο μπορεί να χρησιμοποιηθεί για να γίνει πρόβλεψη της τιμής του y.
- Δεδομένης μιας μεταβλητής y και ενός αριθμού μεταβλητών X1, ..., Xp που μπορεί να σχετίζονται με την y, η ανάλυση γραμμικής παλινδρόμησης μπορεί να εφαρμοστεί για να ποσοτικοποιηθεί η ισχύς της σχέσης μεταξύ της y και των Xj, για να εκτιμηθεί ποια Xj δεν έχει καμία σχέση με την y και για να προσδιοριστεί ποια υποσύνολα των Xj περιέχουν περιττές πληροφορίες σχετικά με την y.
Τα μοντέλα γραμμικής παλινδρόμησης προσπαθούν να καταστήσουν την κάθετη απόσταση μεταξύ της γραμμής και των σημείων δεδομένων (π.χ. τα κατάλοιπα) όσο το δυνατόν μικρότερη. Αυτό ονομάζεται "προσαρμογή της γραμμής στα δεδομένα". Συχνά, τα μοντέλα γραμμικής παλινδρόμησης προσπαθούν να ελαχιστοποιήσουν το άθροισμα των τετραγώνων των υπολοίπων (ελάχιστα τετράγωνα), αλλά υπάρχουν και άλλοι τρόποι προσαρμογής. Περιλαμβάνουν την ελαχιστοποίηση της "έλλειψης προσαρμογής" σε κάποια άλλη νόρμα (όπως στην παλινδρόμηση ελαχίστων απόλυτων αποκλίσεων) ή την ελαχιστοποίηση μιας ποινικοποιημένης έκδοσης της συνάρτησης απώλειας ελαχίστων τετραγώνων, όπως στην παλινδρόμηση κορυφογραμμής. Η προσέγγιση των ελαχίστων τετραγώνων μπορεί επίσης να χρησιμοποιηθεί για την προσαρμογή μοντέλων που δεν είναι γραμμικά. Όπως περιγράφεται παραπάνω, οι όροι "ελαχίστων τετραγώνων" και "γραμμικό μοντέλο" συνδέονται στενά, αλλά δεν είναι συνώνυμα.
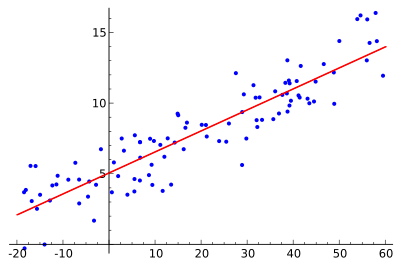
Η ιδέα είναι να βρεθεί η κόκκινη καμπύλη, ενώ τα μπλε σημεία είναι τα πραγματικά δείγματα. Με τη γραμμική παλινδρόμηση όλα τα σημεία μπορούν να συνδεθούν χρησιμοποιώντας μια ενιαία, ευθεία γραμμή. Αυτό το παράδειγμα χρησιμοποιεί απλή γραμμική παλινδρόμηση, όπου ελαχιστοποιείται το τετράγωνο της απόστασης μεταξύ της κόκκινης γραμμής και κάθε σημείου δείγματος.
Χρήση
Οικονομικά
Η γραμμική παλινδρόμηση είναι το κύριο αναλυτικό εργαλείο στα οικονομικά. Για παράδειγμα, χρησιμοποιείται για να μαντέψει τις καταναλωτικές δαπάνες, τις δαπάνες για πάγιες επενδύσεις, τις επενδύσεις σε αποθέματα, τις αγορές των εξαγωγών μιας χώρας, τις δαπάνες για εισαγωγές, τη ζήτηση για την κατοχή ρευστών περιουσιακών στοιχείων, τη ζήτηση εργασίας και την προσφορά εργασίας.
Ερωτήσεις και απαντήσεις
Ερ: Τι είναι η γραμμική παλινδρόμηση;
A: Η γραμμική παλινδρόμηση είναι ένας τρόπος εξέτασης του πώς μεταβάλλεται κάτι όταν μεταβάλλονται άλλα πράγματα χρησιμοποιώντας μαθηματικά. Χρησιμοποιεί μια εξαρτημένη μεταβλητή και μία ή περισσότερες επεξηγηματικές μεταβλητές για να δημιουργήσει μια ευθεία γραμμή, γνωστή ως "γραμμή παλινδρόμησης".
Ερ: Ποια είναι τα πλεονεκτήματα της γραμμικής παλινδρόμησης;
Α: Τα μοντέλα που εξαρτώνται γραμμικά από τις άγνωστες παραμέτρους τους είναι ευκολότερο να προσαρμοστούν από τα μοντέλα που σχετίζονται μη γραμμικά με τις παραμέτρους τους. Επιπλέον, οι στατιστικές ιδιότητες των εκτιμητών που προκύπτουν είναι ευκολότερο να προσδιοριστούν.
Ερ: Ποιες είναι ορισμένες πρακτικές χρήσεις της γραμμικής παλινδρόμησης;
Α: Η γραμμική παλινδρόμηση μπορεί να χρησιμοποιηθεί για την προσαρμογή ενός προγνωστικού μοντέλου σε παρατηρούμενες τιμές (δεδομένα) προκειμένου να γίνουν προβλέψεις, προβλέψεις ή μειώσεις. Μπορεί επίσης να χρησιμοποιηθεί για την ποσοτικοποίηση της ισχύος των σχέσεων μεταξύ μεταβλητών και τον εντοπισμό υποσυνόλων δεδομένων που περιέχουν περιττές πληροφορίες για μια άλλη μεταβλητή.
Ερ: Πώς τα μοντέλα γραμμικής παλινδρόμησης προσπαθούν να ελαχιστοποιήσουν τα σφάλματα;
Α: Τα μοντέλα γραμμικής παλινδρόμησης προσπαθούν να κάνουν την κάθετη απόσταση μεταξύ της γραμμής και των σημείων δεδομένων (τα κατάλοιπα) όσο το δυνατόν μικρότερη. Αυτό επιτυγχάνεται ελαχιστοποιώντας είτε το άθροισμα των τετραγώνων των καταλοίπων (ελάχιστα τετράγωνα), είτε την έλλειψη προσαρμογής σε κάποια άλλη νόρμα (ελάχιστες απόλυτες αποκλίσεις), είτε ελαχιστοποιώντας μια τιμωρημένη εκδοχή της συνάρτησης απωλειών ελαχίστων τετραγώνων (παλινδρόμηση κορυφογραμμής).
Ερ: Είναι δυνατόν τα μοντέλα γραμμικής παλινδρόμησης να μην βασίζονται στα ελάχιστα τετράγωνα;
Α: Ναι, είναι δυνατόν τα μοντέλα γραμμικών παλινδρομήσεων να μην βασίζονται στα ελάχιστα τετράγωνα αλλά αντ' αυτού να χρησιμοποιούν μεθόδους όπως η ελαχιστοποίηση της έλλειψης προσαρμογής σε κάποια άλλη νόρμα (ελάχιστες απόλυτες αποκλίσεις) ή η ελαχιστοποίηση μιας ποινικοποιημένης εκδοχής της συνάρτησης απωλειών ελαχίστων τετραγώνων (ridge regression).
Ερ: Είναι τα "γραμμικό μοντέλο" και "ελαχίστων τετραγώνων" συνώνυμα;
Α: Όχι, δεν είναι συνώνυμα. Παρόλο που συνδέονται στενά, το "γραμμικό μοντέλο" αναφέρεται συγκεκριμένα στη χρήση μιας ευθείας γραμμής, ενώ το "ελάχιστα τετράγωνα" αναφέρεται συγκεκριμένα στην προσπάθεια ελαχιστοποίησης των σφαλμάτων, φροντίζοντας να υπάρχει ελάχιστη κάθετη απόσταση μεταξύ της γραμμής και των σημείων δεδομένων.
ψάχνω