Επιτάχυνση λόγω βαρύτητας
Η επιτάχυνση που αποκτά ένα αντικείμενο λόγω της βαρυτικής δύναμης ονομάζεται επιτάχυνση λόγω βαρύτητας. Η μονάδα SI είναι m/s2 . Η επιτάχυνση λόγω βαρύτητας είναι διάνυσμα, που σημαίνει ότι έχει και μέγεθος και κατεύθυνση. Η επιτάχυνση λόγω βαρύτητας στην επιφάνεια της Γης συμβολίζεται με το γράμμα g. Έχει μια τυπική τιμή που ορίζεται ως 9,80665 m/s2 (32,1740 ft/s2 ). Ωστόσο, η πραγματική επιτάχυνση ενός σώματος σε ελεύθερη πτώση ποικίλλει ανάλογα με την τοποθεσία.
Γιατί τα βαρύτερα αντικείμενα δεν πέφτουν γρηγορότερα από τα ελαφρύτερα αντικείμενα
Ο Ισαάκ Νεύτων βρήκε ότι η συνισταμένη δύναμη ισούται με μάζα επί επιτάχυνση, ή σε σύμβολα, F = m a {\displaystyle F=ma}
. Αυτό μπορεί να αναδιαταχθεί για να δώσει a = F m {\displaystyle a={\frac {F}{m}}\ } } 
. Όσο μεγαλύτερη είναι η μάζα του αντικειμένου που πέφτει, τόσο μεγαλύτερη είναι η δύναμη της βαρυτικής έλξης που το έλκει προς τη Γη. Στην παραπάνω εξίσωση, αυτή είναι F {\displaystyle F}
. Ωστόσο, ο αριθμός των φορών που η δύναμη γίνεται μεγαλύτερη ή μικρότερη είναι ίσος με τον αριθμό των φορών που η μάζα γίνεται μεγαλύτερη ή μικρότερη, έχοντας τον λόγο να παραμένει σταθερός. Σε κάθε περίπτωση, η F m {\displaystyle {\frac {F}{m}}\ }
ακυρώνεται στην ομοιόμορφη επιτάχυνση περίπου 9,8 m/s2 . Αυτό σημαίνει ότι, ανεξάρτητα από τη μάζα τους, όλα τα αντικείμενα που πέφτουν ελεύθερα επιταχύνονται με τον ίδιο ρυθμό.
Σκεφτείτε τα ακόλουθα παραδείγματα:
a = 49 N 5 k g = 9.8 N / k g = 9.8 m / s 2 {\displaystyle a={\frac {49\,\mathrm {N} }{5\,\mathrm {kg} }}\\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} } 
a = 147 N 15 k g = 9.8 N / k g = 9.8 m / s 2 {\displaystyle a={\frac {147\,\mathrm {N} }{15\,\mathrm {kg} }}\\ =9.8\,\mathrm {N/kg} =9.8\,\mathrm {m/s^{2}} } 
Επιφανειακή επιτάχυνση
Ανάλογα με τη θέση, ένα αντικείμενο στην επιφάνεια της Γης πέφτει με επιτάχυνση μεταξύ 9,76 και 9,83 m/s2 (32,0 και 32,3 ft/s2 ).
Η Γη δεν είναι ακριβώς σφαιρική. Μοιάζει με μια "συμπιεσμένη" σφαίρα, με την ακτίνα στον ισημερινό να είναι ελαφρώς μεγαλύτερη από την ακτίνα στους πόλους. Αυτό έχει ως αποτέλεσμα να αυξάνεται ελαφρώς η βαρυτική επιτάχυνση στους πόλους (αφού είμαστε κοντά στο κέντρο της Γης και η βαρυτική δύναμη εξαρτάται από την απόσταση) και να μειώνεται ελαφρώς στον ισημερινό. Επίσης, λόγω της κεντρομόλου επιτάχυνσης, η επιτάχυνση λόγω βαρύτητας είναι ελαφρώς μικρότερη στον ισημερινό από ό,τι στους πόλους. Αλλαγές στην πυκνότητα των πετρωμάτων κάτω από το έδαφος ή η παρουσία βουνών σε κοντινή απόσταση μπορούν να επηρεάσουν ελαφρώς τη βαρυτική επιτάχυνση.
Υψόμετρο
Η επιτάχυνση ενός αντικειμένου μεταβάλλεται με το υψόμετρο. Η μεταβολή της βαρυτικής επιτάχυνσης με την απόσταση από το κέντρο της Γης ακολουθεί τον νόμο του αντίστροφου τετραγώνου. Αυτό σημαίνει ότι η βαρυτική επιτάχυνση είναι αντιστρόφως ανάλογη του τετραγώνου της απόστασης από το κέντρο της Γης. Καθώς η απόσταση διπλασιάζεται, η βαρυτική επιτάχυνση μειώνεται κατά 4. Καθώς η απόσταση τριπλασιάζεται, η βαρυτική επιτάχυνση μειώνεται κατά 9 κ.ο.κ.
βαρυτική επιτάχυνση ∝ 1 απόσταση 2 {\displaystyle {\mbox{βαρυτική επιτάχυνση}}\ \propto \ {\frac {1}{{{\mbox{απόσταση}}^{2}}}}\ }\ } 
βαρυτική επιτάχυνση × απόσταση 2 = k {\displaystyle {\mbox{βαρυτική επιτάχυνση}}\ \times {{\mbox{απόσταση}}^{2}}\ ={k}} 
Στην επιφάνεια της Γης, η επιτάχυνση λόγω της βαρύτητας είναι περίπου 9,8 m/s2 (32 ft/s2 ). Η μέση απόσταση από το κέντρο της Γης είναι 6.371 km (3.959 mi).
k = 9.8 × 6371 2 {\displaystyle {k}={\mbox{9.8}}\ \times {{\mbox{6371}}}^{2}}} 
Χρησιμοποιώντας τη σταθερά k {\displaystyle k} 
, μπορούμε να υπολογίσουμε τη βαρυτική επιτάχυνση σε ένα συγκεκριμένο υψόμετρο.
βαρυτική επιτάχυνση = k απόσταση 2 {\displaystyle {\mbox{βαρυτική επιτάχυνση}}\ ={\frac {k}{{{\mbox{απόσταση}}^{2}}}}} }\ } 
Παράδειγμα: Βρείτε την επιτάχυνση λόγω βαρύτητας 1.000 km (620 mi) πάνω από την επιφάνεια της Γης.
6371 + 1000 = 7371 {\displaystyle 6371+1000=7371} 
∴ Η απόσταση από το κέντρο της Γης είναι 7.371 χιλιόμετρα.
βαρυτική επιτάχυνση = 9.8 × 6371 2 7371 2 ≈ 7.3 {\displaystyle {\mbox{βαρυτική επιτάχυνση}\ ={\frac {{\mbox{9.8}}\ \times {{\mbox{6371}}}^{2}}}{{\mbox{7371}}^{2}}}}\ \approx 7.3} 
∴ Η επιτάχυνση λόγω βαρύτητας 1.000 km (620 mi) πάνω από την επιφάνεια της Γης είναι 7,3 m/s2 (24 ft/s2 ).
Η βαρυτική επιτάχυνση στη γραμμή Kármán, το όριο μεταξύ της ατμόσφαιρας της Γης και του διαστήματος που βρίσκεται σε ύψος 100 χιλιομέτρων, είναι μόνο περίπου 3% χαμηλότερη από ό,τι στο επίπεδο της θάλασσας.
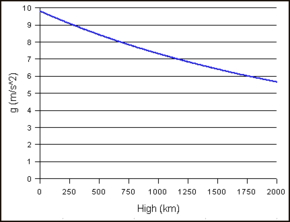
Μεταβολή της βαρυτικής επιτάχυνσης με το ύψος ενός αντικειμένου
Ερωτήσεις και απαντήσεις
Ερ: Τι είναι η επιτάχυνση που οφείλεται στη βαρύτητα;
A: Επιτάχυνση λόγω βαρύτητας είναι η επιτάχυνση που αποκτά ένα αντικείμενο λόγω της βαρυτικής δύναμης.
Ερ: Ποια είναι η μονάδα SI της επιτάχυνσης λόγω βαρύτητας;
Α: Η μονάδα SI της επιτάχυνσης λόγω βαρύτητας είναι m/s2.
Ερ: Η επιτάχυνση λόγω βαρύτητας είναι κλιμάκιο ή διάνυσμα;
Α: Η επιτάχυνση λόγω βαρύτητας είναι διάνυσμα επειδή έχει και μέγεθος και κατεύθυνση.
Ερ: Ποιο είναι το σύμβολο που χρησιμοποιείται για την αναπαράσταση της επιτάχυνσης λόγω βαρύτητας στην επιφάνεια της Γης;
Α: Το σύμβολο που χρησιμοποιείται για την αναπαράσταση της επιτάχυνσης λόγω της βαρύτητας στην επιφάνεια της Γης είναι το g.
Ερ: Ποια είναι η τυπική τιμή της επιτάχυνσης λόγω της βαρύτητας στην επιφάνεια της Γης;
Α: Η τυπική τιμή της επιτάχυνσης λόγω της βαρύτητας στην επιφάνεια της Γης είναι 9,80665 m/s2 (32,1740 ft/s2).
Ερ: Η πραγματική επιτάχυνση ενός σώματος σε ελεύθερη πτώση μεταβάλλεται ανάλογα με την τοποθεσία;
Α: Ναι, η πραγματική επιτάχυνση ενός σώματος σε ελεύθερη πτώση μεταβάλλεται ανάλογα με τη θέση.
Ερ: Ποιος είναι ο ορισμός της επιτάχυνσης λόγω βαρύτητας;
Α: Η επιτάχυνση λόγω βαρύτητας είναι η επιτάχυνση που αποκτά ένα σώμα λόγω της βαρυτικής δύναμης και παριστάνεται με το γράμμα g με τυπική τιμή 9,80665 m/s2 στην επιφάνεια της Γης, ενώ η πραγματική επιτάχυνση μπορεί να ποικίλλει ανάλογα με την τοποθεσία.
