Φράκταλ

Παραδείγματα

Υπάρχουν πολλοί τύποι φράκταλ, φτιαγμένοι με μεγάλη ποικιλία τρόπων. Ένα παράδειγμα είναι το τρίγωνο Sierpinski, όπου υπάρχει άπειρος αριθμός μικρών τριγώνων μέσα στο μεγάλο τρίγωνο. Ένα άλλο παράδειγμα είναι το σύνολο Mandelbrot, που πήρε το όνομά του από τον Benoît Mandelbrot. Το τρίγωνο Sierpinksi κατασκευάζεται χρησιμοποιώντας μοτίβα, αλλά το σύνολο Mandelbrot βασίζεται σε μια εξίσωση.

Υπάρχουν επίσης πολλά φυσικά παραδείγματα φράκταλ στη φύση, όπως δέντρα, νιφάδες χιονιού, μερικά λαχανικά και ακτογραμμές.

Η καμπύλη Koch

Η καμπύλη Koch είναι ένα απλό παράδειγμα φράκταλ. Αρχικά, ξεκινήστε με ένα τμήμα μιας ευθείας γραμμής - που ονομάζεται ευθύγραμμο τμήμα. Κόψτε την ευθεία σε 3 κομμάτια ίδιου μεγέθους. Ξεφορτωθείτε το μεσαίο από αυτά τα κομμάτια, και βάλτε μέσα το πάνω μέρος ενός τριγώνου με πλευρές που έχουν το ίδιο μήκος με το κομμάτι που θα κόψετε. Τώρα έχουμε 4 ευθύγραμμα τμήματα τα οποία εφάπτονται στα άκρα. Μπορούμε τώρα να κάνουμε ό,τι κάναμε στο πρώτο τμήμα σε κάθε ένα από τα 4 κομμάτια. Μπορούμε τώρα να κάνουμε το ίδιο πράγμα ξανά και ξανά σε όλα τα κομμάτια που καταλήγουμε. Τώρα το κάνουμε αυτό για πάντα και κοιτάμε τι έχουμε στο τέλος.

Το μήκος της καμπύλης Koch είναι άπειρο και το εμβαδόν της καμπύλης Koch είναι μηδέν. Αυτό είναι αρκετά περίεργο. Ένα ευθύγραμμο τμήμα (με διάσταση 1) μπορεί να έχει μήκος 1, αλλά έχει εμβαδόν 0. Ένα τετράγωνο μήκους 1 και πλάτους 1 (με διάσταση 2) θα έχει εμβαδόν 1 και μήκος άπειρο.

Διάσταση ομοιότητας

Έτσι, η καμπύλη Koch φαίνεται να είναι μεγαλύτερη από κάτι της διάστασης 1 και μικρότερη από κάτι της διάστασης 2. Η ιδέα της διάστασης της ομοιότητας είναι να δώσει μια διάσταση που δίνει μια καλύτερη ιδέα του μήκους ή του εμβαδού για τα φράκταλ. Έτσι, για μια καμπύλη Koch, θέλουμε μια διάσταση μεταξύ 1 και 2.

Η καμπύλη Koch μπορεί να κοπεί σε τέσσερα κομμάτια, καθένα από τα οποία είναι 1 3 {\displaystyle {\frac {\1}{3}}} του μεγέθους του πρωτοτύπου. Ονομάζουμε τον αριθμό των κομματιών στα οποία μπορεί να κοπεί ένα fractal σε N {\displaystyle N} , και ονομάζουμε τη διαφορά μεγέθους B {\displaystyle B} . Τα βάζουμε στην εξίσωση:

log N - log B {\displaystyle {\frac {\log N}{-\log B}}}

Όπου log {\displaystyle \log } είναι ο λογάριθμος ενός αριθμού. Αυτός ο αριθμός είναι η διάσταση Hausdorff του φράκταλ. Στην καμπύλη Koch, είναι log 4 - log 1 3 = 1,2619... {\displaystyle {\frac {\log 4}{-\log {\frac {1}{3}}}}=1.2619... } όπως θέλαμε.

Η καμπύλη Koch είναι ένα από τα απλούστερα σχήματα φράκταλ και έτσι η διάστασή της είναι εύκολο να υπολογιστεί. Η διάσταση ομοιότητάς της και η διάσταση Hausdorff είναι και οι δύο ίδιες. Αυτό δεν ισχύει για τα πιο πολύπλοκα φράκταλ.

Koch χιονονιφάδα

Η χιονονιφάδα Koch (ή αστέρι Koch) είναι η ίδια με την καμπύλη Koch, με τη διαφορά ότι ξεκινά με ένα ισόπλευρο τρίγωνο αντί για ένα ευθύγραμμο τμήμα.

Πώς να φτιάξετε την καμπύλη Koch

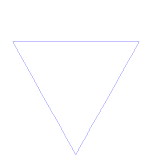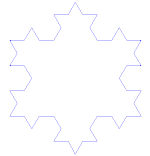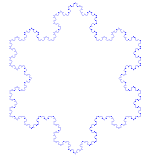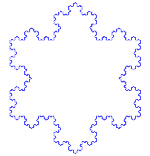
Χρησιμοποιεί το

Τα φράκταλ έχουν πολλές εφαρμογές, π.χ. στη βιολογία (πνεύμονες, νεφρά, μεταβλητότητα καρδιακού ρυθμού, κ.λπ...), στους σεισμούς, στα χρηματοοικονομικά, όπου σχετίζονται με τις λεγόμενες κατανομές βαριάς ουράς, και στη φυσική. Αυτό δείχνει ότι τα fractals πρέπει να μελετηθούν για να κατανοήσουμε γιατί τα fractals είναι τόσο συχνά στη φύση.

Ορισμένα φράκταλ υπάρχουν μόνο για καλλιτεχνικούς λόγους, αλλά άλλα είναι πολύ χρήσιμα. Τα φράκταλ είναι πολύ αποδοτικά σχήματα για ραδιοφωνικές κεραίες και χρησιμοποιούνται στα τσιπ υπολογιστών για την αποτελεσματική σύνδεση όλων των εξαρτημάτων. Επίσης, οι ακτογραμμές μπορούν να θεωρηθούν ως φράκταλ.