Συνάρτηση πυκνότητας πιθανότητας

Η συνάρτηση πυκνότητας πιθανότητας είναι μια συνάρτηση που μπορεί να οριστεί για οποιαδήποτε συνεχή κατανομή πιθανότητας. Το ολοκλήρωμα της συνάρτησης πυκνότητας πιθανότητας στο διάστημα [ a , b ] {\displaystyle [a,b]} $[a,b]$ δίνει την πιθανότητα μια δεδομένη τυχαία μεταβλητή με τη δεδομένη πυκνότητα να περιέχεται στο παρεχόμενο διάστημα.

Η συνάρτηση πυκνότητας πιθανότητας είναι απαραίτητη για να μπορούμε να εργαστούμε με συνεχείς κατανομές. Η ρίψη ενός ζαριού θα δώσει τους αριθμούς 1 έως 6, με πιθανότητα 1 6 {\displaystyle {\tfrac {1}{6}}} ${\tfrac {1}{6}}$ , αλλά αυτό δεν είναι μια συνεχής συνάρτηση, καθώς μόνο οι αριθμοί 1 έως 6 είναι δυνατοί. Αντίθετα, δύο άνθρωποι δεν θα έχουν το ίδιο ύψος ή το ίδιο βάρος. Χρησιμοποιώντας μια συνάρτηση πυκνότητας πιθανότητας, είναι δυνατόν να προσδιοριστεί η πιθανότητα για ανθρώπους μεταξύ 180 εκατοστών και 181 εκατοστών, ή μεταξύ 80 κιλών και 81 κιλών, παρόλο που υπάρχουν άπειρες τιμές μεταξύ αυτών των δύο ορίων.

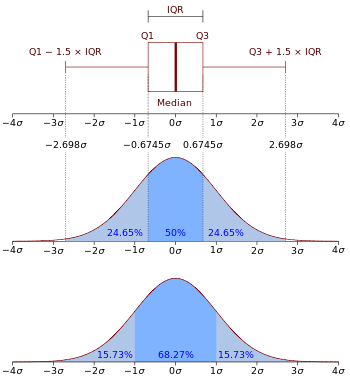
Boxplot και συνάρτηση πυκνότητας πιθανότητας μιας κανονικής κατανομής N(0, σ2) .

Ερωτήσεις και απαντήσεις

Ερ: Τι είναι η συνάρτηση πυκνότητας πιθανότητας;

A: Μια συνάρτηση πυκνότητας πιθανότητας είναι μια συνάρτηση που χαρακτηρίζει οποιαδήποτε συνεχή κατανομή πιθανότητας.

Ερ: Πώς γράφεται η συνάρτηση πυκνότητας πιθανότητας μιας τυχαίας μεταβλητής Χ;

A: Η συνάρτηση πυκνότητας πιθανότητας της Χ γράφεται μερικές φορές ως f_X(x).

Ερ: Τι αντιπροσωπεύει το ολοκλήρωμα της συνάρτησης πυκνότητας πιθανότητας;

Α: Το ολοκλήρωμα της συνάρτησης πυκνότητας πιθανότητας αναπαριστά την πιθανότητα μια δεδομένη τυχαία μεταβλητή με τη δεδομένη πυκνότητα να περιέχεται σε ένα παρεχόμενο διάστημα.

Ερ: Είναι η συνάρτηση πυκνότητας πιθανότητας πάντα μη αρνητική σε όλο το πεδίο εφαρμογής της;

Α: Ναι, εξ ορισμού, η συνάρτηση πυκνότητας πιθανότητας είναι μη αρνητική σε όλο το πεδίο εφαρμογής της.

Ερ: Η ολοκλήρωση σε ένα διάστημα καταλήγει στο άθροισμα 1;

Απάντηση: Ναι, η ολοκλήρωση σε ένα διάστημα έχει άθροισμα 1.

Ερ: Τι είδους κατανομή χαρακτηρίζει μια συνάρτηση πυκνότητας πιθανότητας;

Α: Μια Συνάρτηση Πυκνότητας Πιθανότητας χαρακτηρίζει κάθε συνεχή κατανομή πιθανότητας.