Πιθανότητα
Οι πιθανότητες αποτελούν μέρος των εφαρμοσμένων μαθηματικών. Έχει να κάνει με την τύχη, τη μελέτη των πραγμάτων που μπορεί να συμβούν ή να μην συμβούν.
Για παράδειγμα, χρησιμοποιώντας τις πιθανότητες, μπορείτε να δείξετε ότι αν πετάξετε ένα νόμισμα στον αέρα και το αφήσετε να προσγειωθεί, τις μισές φορές θα προσγειωθεί με τη μία πλευρά προς τα πάνω και τις μισές φορές με την άλλη πλευρά προς τα πάνω. Πολλά κέρματα έχουν στη μία πλευρά τους την εικόνα του προσώπου ενός διάσημου προσώπου και στην άλλη πλευρά κάτι άλλο. Συχνά οι άνθρωποι αποκαλούν την πλευρά με το πρόσωπο "κορώνα" και την άλλη πλευρά "γράμματα".
Η πιθανότητα (p) ενός γεγονότος είναι πάντα μεταξύ μηδέν (αδύνατο) και ένα (βέβαιο).
Αν ρίξουμε ένα ζάρι (πληθυντικός: ζάρια), τότε η πιθανότητα να πέσει στο 1 είναι 1/6 (Αυτό συμβαίνει επειδή υπάρχουν 6 αριθμοί σε ένα ζάρι). Επίσης, η πιθανότητα να πέσει στο 2 είναι 1/6. Αυτό συμβαίνει επειδή μπορεί να πέσει στο 1, 2, 3, 4, 5 ή 6. Η πιθανότητα να προσγειωθεί οποιοσδήποτε αριθμός μεταξύ 1 και 6 είναι 1. Κάθε φορά που ρίχνουμε το ζάρι, θα προσγειώνεται πάντα σε έναν αριθμό μεταξύ 1 και 6.
Η πιθανότητα μπορεί να υπολογιστεί με τη χρήση μαθηματικών. Για παράδειγμα, αν ρίξετε έξι ζάρια, η πιθανότητα να πάρετε έναν αριθμό μεγαλύτερο του δέκα δεν είναι προφανής, αλλά μπορεί να υπολογιστεί με τη χρήση των μαθηματικών και της επιστήμης.
Ένα από τα πιο ενδιαφέροντα πράγματα σχετικά με την τύχη είναι ότι για να υπολογίσετε την πιθανότητα δύο πράγματα να συμβούν και τα δύο πολλαπλασιάζετε τις δύο πιθανότητες μαζί. Για παράδειγμα, ας υποθέσουμε ότι θέλετε να μάθετε την πιθανότητα να ρίξετε δύο ζάρια και να πάρετε έναν συγκεκριμένο συνδυασμό (θα μπορούσε να είναι δύο 6άρια ή ένα 3 και μετά ένα 5, απλά δύο οποιονδήποτε). Η πιθανότητα να πάρετε ένα 3 είναι μία στις έξι (⅙) και η πιθανότητα να πάρετε ένα 5 είναι επίσης μία στις έξι, οπότε οι πιθανότητες να πάρετε ένα 3 και μετά ένα 5 είναι ⅙×⅙=⅟36. Αν αυτός ο αριθμός εκφραστεί ως κάτι μεταξύ 0 και 1, ισούται με 0,027...7, που είναι αρκετά χαμηλό. Η πιθανότητα να πάρετε ένα 3, μετά ένα 5 και μετά ένα 2 θα ήταν ⅙×⅙×⅙×⅙=⅟216 ή 0,00463, που είναι πολύ μικρότερη πιθανότητα.
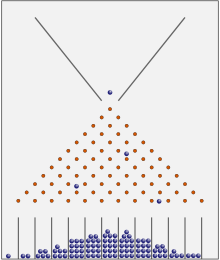
Σε μια μηχανή φασολιών ή σε ένα κουτί Galton οι περισσότερες μπάλες καταλήγουν κοντά στο κέντρο. Μακροπρόθεσμα, θα παρουσιάσουν κανονική κατανομή.
Ιδέες των πιθανοτήτων
Άνθρωποι όπως ο Jacob Bernoulli, ο Pierre-Simon Laplace ή ο Christiaan Huygens χρησιμοποιούσαν τη λέξη πιθανότητα, όπως περιγράφεται παραπάνω. Άλλοι άνθρωποι σκέφτονταν τις συχνότητες- η έννοια της πιθανότητας ονομάζεται συνήθως πιθανότητα συχνότητας.
Σχετικές σελίδες
- Κατάλογος μαθηματικών θεμάτων
- Θεωρία πιθανοτήτων
Ερωτήσεις και απαντήσεις
Q: Τι είναι η πιθανότητα;
A: Η πιθανότητα είναι ένα μέρος των εφαρμοσμένων μαθηματικών που ασχολείται με τη μελέτη των πραγμάτων που μπορεί να συμβούν ή να μην συμβούν.
Ερ: Πώς μπορεί να εκφραστεί η πιθανότητα;
A: Η πιθανότητα μπορεί να εκφραστεί ως ένας αριθμός μεταξύ μηδέν (αδύνατο) και ένα (βέβαιο).
Ερ: Ποιο είναι ένα παράδειγμα χρήσης των πιθανοτήτων;
Α: Ένα παράδειγμα χρήσης της πιθανότητας είναι να δείξουμε ότι πετώντας ένα νόμισμα στον αέρα και αφήνοντάς το να προσγειωθεί, τις μισές φορές θα προσγειωθεί με τη μία πλευρά προς τα πάνω και τις μισές φορές με την άλλη πλευρά προς τα πάνω.
Ερ: Πώς υπολογίζετε την πιθανότητα να ρίξετε δύο ζάρια και να πάρετε έναν συγκεκριμένο συνδυασμό;
Α: Για να υπολογίσετε την πιθανότητα να ρίξετε δύο ζάρια και να πάρετε έναν συγκεκριμένο συνδυασμό, θα πολλαπλασιάσετε τις δύο πιθανότητές τους μαζί. Για παράδειγμα, αν θέλατε να μάθετε την πιθανότητα να πάρετε ένα 3 και μετά ένα 5, θα ήταν 1/6 x 1/6 = 1/36.
Ερ: Σε τι αναφέρεται η λέξη "γράμματα" όταν μιλάμε για κέρματα;
Α: Όταν μιλάμε για κέρματα, το "γράμματα" αναφέρεται στην πλευρά που δεν έχει την όψη ή την εικόνα πάνω της.
Ερ: Πόσο πιθανό είναι να ρίξουμε έξι ζάρια και να πάρουμε έναν αριθμό μεγαλύτερο του δέκα; Α: Η πιθανότητα να ρίξεις έξι ζάρια και να πάρεις έναν αριθμό μεγαλύτερο του δέκα μπορεί να υπολογιστεί χρησιμοποιώντας μαθηματικά και επιστήμη, αλλά δεν είναι προφανής.
Ερ: Τι συμβαίνει όταν πολλαπλασιάζετε δύο πιθανότητες μαζί;
Α: Όταν πολλαπλασιάζετε δύο πιθανότητες μαζί, υπολογίζετε την πιθανότητα να συμβούν και τα δύο πράγματα ταυτόχρονα.
ψάχνω