Συνάρτηση
Στα μαθηματικά, μια συνάρτηση είναι ένα μαθηματικό αντικείμενο που παράγει μια έξοδο, όταν του δίνεται μια είσοδος - μπορεί να είναι ένας αριθμός, ένα διάνυσμα ή οτιδήποτε μπορεί να υπάρχει μέσα σε ένα σύνολο πραγμάτων.
Έτσι, μια συνάρτηση είναι σαν μια μηχανή, η οποία λαμβάνει τιμές x και επιστρέφει μια έξοδο y. Το σύνολο όλων των τιμών που μπορεί να έχει το x ονομάζεται πεδίο εφαρμογής. Το σύνολο που περιέχει κάθε τιμή που μπορεί να έχει το y ονομάζεται codomain.
Αν συμβαίνει αυτό, λέμε ότι το y είναι συνάρτηση του x και γράφουμε y =f(x). f είναι το όνομα της συνάρτησης και γράφουμε f : X → Y {\displaystyle f:X\to Y} 
Ένα παράδειγμα συνάρτησης είναι η f(x)=x+1. Δίνει κανείς έναν φυσικό αριθμό x {\displaystyle x}


Μεταφορές
Πίνακες

Οι είσοδοι και οι έξοδοι μπορούν να τοποθετηθούν σε έναν πίνακα όπως στην εικόνα- αυτό είναι εύκολο αν δεν υπάρχουν πολλά δεδομένα.
Γραφήματα

Στην εικόνα φαίνεται ότι τόσο το 2 όσο και το 3 έχουν αντιστοιχιστεί με το c- αυτό δεν επιτρέπεται στην αντίθετη κατεύθυνση, το 2 δεν θα μπορούσε να βγάλει το c και το d, κάθε είσοδος μπορεί να έχει μόνο μία έξοδο. Όλες οι f ( x ) {\displaystyle f(x)} 


Ιστορία
Στη δεκαετία του 1690 ο Gottfried Leibniz και ο Johann Bernoulli χρησιμοποίησαν τη λέξη συνάρτηση με γράμματα μεταξύ τους, οπότε η σύγχρονη έννοια ξεκίνησε ταυτόχρονα με τον λογισμό.
Το 1748 ο Leonhard Euler έδωσε: "Μια συνάρτηση μιας μεταβλητής ποσότητας είναι μια αναλυτική έκφραση που αποτελείται με οποιονδήποτε τρόπο από τη μεταβλητή ποσότητα και αριθμούς ή σταθερές ποσότητες." και στη συνέχεια το 1755: "Αν κάποιες ποσότητες εξαρτώνται κατά τέτοιο τρόπο από άλλες ποσότητες, ώστε αν οι τελευταίες μεταβληθούν, οι πρώτες υφίστανται μεταβολή, τότε οι πρώτες ποσότητες ονομάζονται συναρτήσεις των δεύτερων. Αυτός ο ορισμός εφαρμόζεται μάλλον ευρέως και περιλαμβάνει όλους τους τρόπους με τους οποίους μια ποσότητα θα μπορούσε να καθορίζεται από μια άλλη. Αν, επομένως, το x δηλώνει μια μεταβλητή ποσότητα, τότε όλες οι ποσότητες που εξαρτώνται από το x με οποιονδήποτε τρόπο ή προσδιορίζονται από αυτό, ονομάζονται συναρτήσεις του x." που είναι πολύ σύγχρονο.
Συνήθως, στον Ντίριχλετ αποδίδεται η εκδοχή που χρησιμοποιήθηκε στα σχολεία μέχρι το δεύτερο μισό του 20ού αιώνα: "Η y είναι συνάρτηση μιας μεταβλητής x, που ορίζεται στο διάστημα a < x < b, αν σε κάθε τιμή της μεταβλητής x στο διάστημα αυτό αντιστοιχεί μια ορισμένη τιμή της μεταβλητής y. Επίσης, δεν έχει σημασία με ποιον τρόπο εγκαθιδρύεται αυτή η αντιστοιχία".
Το 1939, ο Μπουρμπακί γενίκευσε τον ορισμό του Ντίριχλετ και έδωσε μια θεωρητική εκδοχή του ορισμού ως αντιστοιχία μεταξύ εισροών και εκροών- αυτό χρησιμοποιήθηκε στα σχολεία από το 1960 περίπου.
Τελικά το 1970, ο Bourbaki έδωσε τον σύγχρονο ορισμό ως ένα τρίπτυχο f = ( X , Y , F ) {\displaystyle f=(X,Y,F)} 



Τύποι λειτουργιών
- Στοιχειώδεις συναρτήσεις - Οι συναρτήσεις που συνήθως μελετώνται στο σχολείο: κλάσματα, τετραγωνικές ρίζες, ημιτόνιο, συνημίτονο και εφαπτομένη και ορισμένες άλλες συναρτήσεις.
- Μη στοιχειώδεις συναρτήσεις - Οι περισσότερες από αυτές δεν χρησιμοποιούν πράξεις που δεν μαθαίνουμε στο σχολείο (όπως + ή -, ή δυνάμεις). Πολλά ολοκληρώματα είναι μη στοιχειώδεις.
- Αντίστροφες συναρτήσεις - Συναρτήσεις που αναιρούν μια άλλη συνάρτηση. Για παράδειγμα: αν η F(x) είναι η αντίστροφη της f(x)=y, τότε F(y)=x. Δεν έχουν όλες οι συναρτήσεις αντίστροφες.
- Ειδικές λειτουργίες: Συναρτήσεις που έχουν ονόματα. Για παράδειγμα: ημίτονο, συνημίτονο και εφαπτομένη. Συναρτήσεις όπως f(x)=3x (τρεις φορές το x) δεν ονομάζονται ειδικές συναρτήσεις. Μπορούν να είναι στοιχειώδεις, μη στοιχειώδεις ή αντίστροφες.
Ερωτήσεις και απαντήσεις
Ερ: Τι είναι μια συνάρτηση στα μαθηματικά;
A: Μια συνάρτηση στα μαθηματικά είναι ένα αντικείμενο που παράγει μια έξοδο όταν του δίνεται μια είσοδος, η οποία μπορεί να είναι ένας αριθμός, ένα διάνυσμα ή οτιδήποτε μπορεί να υπάρχει μέσα σε ένα σύνολο πραγμάτων.
Ερ: Ποια είναι τα δύο σύνολα που σχετίζονται με τις συναρτήσεις;
Α: Το σύνολο όλων των τιμών που μπορεί να έχει το x ονομάζεται πεδίο ορισμού (domain) και το σύνολο που περιέχει κάθε τιμή που μπορεί να έχει το y ονομάζεται συν-πεδίο ορισμού (codomain).
Ερ: Πώς συμβολίζονται συχνά οι συναρτήσεις;
Α: Οι συναρτήσεις συχνά συμβολίζονται με πλάγια γράμματα όπως f, g, h.
Ερ: Πώς αναπαριστούμε μια συνάρτηση;
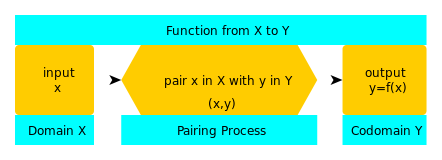
Α: Αναπαριστούμε μια συνάρτηση γράφοντας y = f(x), όπου f είναι το όνομα της συνάρτησης και γράφουμε f : X → Y (συνάρτηση από το X στο Y) για να αναπαραστήσουμε τα τρία μέρη της συνάρτησης - το πεδίο ορισμού (X), το συν-πεδίο ορισμού (Y) και τη διαδικασία αντιστοίχισης (το βέλος).
Ερώτηση: Μπορείτε να δώσετε ένα παράδειγμα μιας συνάρτησης;
Α: Ένα παράδειγμα συνάρτησης είναι η f(x) = x + 1. Δίνει κανείς έναν φυσικό αριθμό x ως είσοδο και παίρνει τον φυσικό αριθμό y που είναι x + 1. Για παράδειγμα, δίνοντας το 3 ως είσοδο στην f έχουμε ως έξοδο το 4.
Ερ: Κάθε συνάρτηση πρέπει να είναι εξίσωση;
Α: Όχι, δεν χρειάζεται κάθε συνάρτηση να είναι εξίσωση. Η βασική ιδέα πίσω από τις συναρτήσεις είναι ότι οι είσοδοι και οι έξοδοι αντιστοιχίζονται με κάποιο τρόπο - ακόμη και αν αυτό μπορεί να είναι πολύ περίπλοκο.
ψάχνω