Κύκλος
Ο κύκλος είναι ένα στρογγυλό, δισδιάστατο σχήμα. Όλα τα σημεία στην άκρη του κύκλου βρίσκονται στην ίδια απόσταση από το κέντρο.
Η ακτίνα ενός κύκλου είναι μια ευθεία από το κέντρο του κύκλου σε ένα σημείο της πλευράς του. Οι μαθηματικοί χρησιμοποιούν το γράμμα r για το μήκος της ακτίνας ενός κύκλου. Το κέντρο ενός κύκλου είναι το σημείο στο κέντρο του.
Η διάμετρος (που σημαίνει "σε όλη την έκταση") ενός κύκλου είναι μια ευθεία γραμμή που περνάει από τη μια πλευρά στην απέναντι και ακριβώς από το κέντρο του κύκλου. Οι μαθηματικοί χρησιμοποιούν το γράμμα d για το μήκος αυτής της γραμμής. Η διάμετρος ενός κύκλου είναι ίση με το διπλάσιο της ακτίνας του (d ίσον 2 φορές το r).
d = 2 r {\displaystyle d=2\ r}
Η περιφέρεια (που σημαίνει "όλη η περιφέρεια") ενός κύκλου είναι η γραμμή που περνάει γύρω από το κέντρο του κύκλου. Οι μαθηματικοί χρησιμοποιούν το γράμμα C για το μήκος αυτής της γραμμής.
Ο αριθμός π (που γράφεται ως το ελληνικό γράμμα π) είναι ένας πολύ χρήσιμος αριθμός. Είναι το μήκος της περιφέρειας διαιρούμενο με το μήκος της διαμέτρου (π ίσον C διαιρούμενο με d). Ως κλάσμα ο αριθμός π ισούται με περίπου 22⁄7 ή 335/113 (που είναι πιο κοντά) και ως αριθμός είναι περίπου 3,1415926535.
Το εμβαδόν, α, στο εσωτερικό ενός κύκλου είναι ίσο με την ακτίνα πολλαπλασιασμένη επί τον εαυτό της και στη συνέχεια πολλαπλασιασμένη επί π (α ίσο με π επί r επί r).

Ένας κύκλος
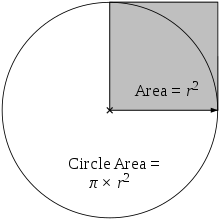
Το εμβαδόν του κύκλου είναι ίσο με το π-πλάσιο του εμβαδού του γκρι τετραγώνου.
Υπολογισμός π
Το π μπορεί να μετρηθεί σχεδιάζοντας έναν μεγάλο κύκλο και στη συνέχεια μετρώντας τη διάμετρο (d) και την περιφέρεια (C). Αυτό συμβαίνει επειδή η περιφέρεια ενός κύκλου είναι πάντα π φορές η διάμετρός του.
π = C d {\displaystyle \pi ={\frac {C}{d}}}
Το π μπορεί επίσης να υπολογιστεί μόνο με τη χρήση μαθηματικών μεθόδων. Οι περισσότερες μέθοδοι που χρησιμοποιούνται για τον υπολογισμό της τιμής του π έχουν επιθυμητές μαθηματικές ιδιότητες. Ωστόσο, είναι δύσκολο να κατανοηθούν χωρίς να γνωρίζει κανείς τριγωνομετρία και λογισμό. Ωστόσο, ορισμένες μέθοδοι είναι αρκετά απλές, όπως αυτή η μορφή της σειράς Gregory-Leibniz:
π = 4 1 - 4 3 + 4 5 - 4 7 + 4 9 - 4 11 ⋯ {\displaystyle \pi ={\frac {4}{1}}-{\frac {4}{3}}+{\frac {4}{5}}}-{\frac {4}{7}}+{\frac {4}{9}}-{\frac {4}{11}}\cdots }
Ενώ η σειρά αυτή είναι εύκολο να γραφτεί και να υπολογιστεί, δεν είναι εύκολο να δούμε γιατί ισούται με π. Μια πιο κατανοητή προσέγγιση είναι να σχεδιάσουμε έναν νοητό κύκλο ακτίνας r με κέντρο την αρχή. Τότε κάθε σημείο (x,y) του οποίου η απόσταση d από την αρχή είναι μικρότερη από το r, που υπολογίζεται από το πυθαγόρειο θεώρημα, θα βρίσκεται μέσα στον κύκλο:
d = x 2 + y 2 {\displaystyle d={\sqrt {x^{2}+y^{2}}}}
Η εύρεση ενός συνόλου σημείων εντός του κύκλου επιτρέπει την εκτίμηση του εμβαδού Α του κύκλου. Για παράδειγμα, χρησιμοποιώντας ακέραιες συντεταγμένες για ένα μεγάλο r. Δεδομένου ότι το εμβαδόν Α ενός κύκλου είναι π φορές το τετράγωνο της ακτίνας, το π μπορεί να προσεγγιστεί χρησιμοποιώντας:
π = A r 2 {\displaystyle \pi ={\frac {A}{r^{2}}}}
Σχετικές σελίδες
- Σφαίρα
Ερωτήσεις και απαντήσεις
Ε: Τι είναι ο κύκλος;
A: Ο κύκλος είναι ένα στρογγυλό, δισδιάστατο σχήμα. Όλα τα σημεία στην άκρη του κύκλου βρίσκονται στην ίδια απόσταση από το κέντρο.
Ερ: Τι χρησιμοποιούν οι μαθηματικοί για να αναπαραστήσουν το μήκος της ακτίνας ενός κύκλου;
Α: Οι μαθηματικοί χρησιμοποιούν το γράμμα r για το μήκος της ακτίνας ενός κύκλου.
Ερ: Τι γράφεται ως Ο στους κύκλους;
Α: Το κέντρο ενός κύκλου γράφεται συχνά ως Ο.
Ερ: Πόσο μεγάλη είναι η διάμετρος ενός κύκλου;
Α: Η διάμετρος (που σημαίνει "σε όλο το μήκος") ενός κύκλου είναι μια ευθεία γραμμή που περνάει από τη μια πλευρά στην απέναντι και ακριβώς από το κέντρο του κύκλου. Είναι ίση με το διπλάσιο της ακτίνας του (d ισούται με 2 φορές το r).
Ερ: Ποιο γράμμα χρησιμοποιούν οι μαθηματικοί για να αναπαραστήσουν την περιφέρεια;
Α: Οι μαθηματικοί χρησιμοποιούν το C για την περιφέρεια, που σημαίνει "γύρω-γύρω".
Ερ: Πώς μπορούμε να υπολογίσουμε το εμβαδόν στο εσωτερικό ενός κύκλου;
Α: Το εμβαδόν, Α, στο εσωτερικό ενός κύκλου μπορεί να υπολογιστεί πολλαπλασιάζοντας την ακτίνα του με τον εαυτό του και στη συνέχεια πολλαπλασιάζοντας με το ً (το Α ισούται με ً επί r επί r).
ψάχνω




