Κύλινδρος (γεωμετρία)
Ο κύλινδρος είναι ένα από τα βασικότερα καμπύλα γεωμετρικά σχήματα, με την επιφάνεια να σχηματίζεται από τα σημεία σε σταθερή απόσταση από ένα δεδομένο ευθύγραμμο τμήμα, γνωστό ως άξονας του κυλίνδρου. Το σχήμα μπορεί να θεωρηθεί ως κυκλικό πρίσμα. Τόσο η επιφάνεια όσο και το στερεό σχήμα που δημιουργείται στο εσωτερικό του μπορούν να ονομαστούν κύλινδρος. Η επιφάνεια και ο όγκος ενός κυλίνδρου είναι γνωστά από την αρχαιότητα.
Στη διαφορική γεωμετρία, ο κύλινδρος ορίζεται ευρύτερα ως οποιαδήποτε επιφάνεια που καλύπτεται από μια μονοπαραμετρική οικογένεια παράλληλων ευθειών. Ένας κύλινδρος του οποίου η διατομή είναι έλλειψη, παραβολή ή υπερβολή ονομάζεται ελλειπτικός κύλινδρος, παραβολικός κύλινδρος ή υπερβολικός κύλινδρος αντίστοιχα.
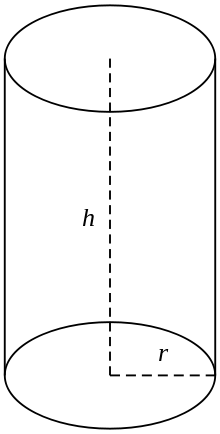
Ένας ορθός κυκλικός κύλινδρος
Κοινή χρήση
Στην κοινή χρήση ως κύλινδρος νοείται η πεπερασμένη τομή ενός ορθού κυκλικού κυλίνδρου, δηλαδή του κυλίνδρου με τις γενέτειρες κάθετες στις βάσεις, με τα άκρα του κλειστά ώστε να σχηματίζουν δύο κυκλικές επιφάνειες, όπως στο σχήμα (δεξιά). Αν ο κύλινδρος έχει ακτίνα r και μήκος (ύψος) h, τότε ο όγκος του δίνεται από:
V = πrh2
και η επιφάνειά του είναι:
- το εμβαδόν της κορυφής (πr2) +
- το εμβαδόν του πυθμένα (πr2) +
- το εμβαδόν της πλευράς (2πrh).
Επομένως, χωρίς το πάνω ή το κάτω μέρος (πλευρική επιφάνεια), η επιφάνεια είναι:
A = 2πrh.
Με το πάνω και το κάτω μέρος, η επιφάνεια είναι:
A = 2πr 2+ 2πrh = 2πr(r + h).
Για δεδομένο όγκο, ο κύλινδρος με τη μικρότερη επιφάνεια έχει h = 2r. Για δεδομένη επιφάνεια, ο κύλινδρος με τον μεγαλύτερο όγκο έχει h = 2r, δηλαδή ο κύλινδρος χωράει σε κύβο (ύψος = διάμετρος).
Τόμος
Έχοντας έναν ορθογώνιο κυκλικό κύλινδρο με ύψος h μονάδες και μια βάση ακτίνας r μονάδες με τους άξονες συντεταγμένων να επιλέγονται έτσι ώστε η αρχή να βρίσκεται στο κέντρο της μιας βάσης και το ύψος να μετράται κατά μήκος του θετικού άξονα x. Μια επίπεδη τομή σε απόσταση x μονάδων από την αρχή έχει εμβαδόν A(x) τετραγωνικών μονάδων όπου
A ( x ) = π r {\displaystyle2 A(x)=\pi r^{2}}
ή
A ( y ) = π r {\displaystyle2 A(y)=\pi r^{2}}
Ένα στοιχείο όγκου, είναι ένας ορθός κύλινδρος με εμβαδόν βάσης Awi τετραγωνικές μονάδες και πάχος Δxi μονάδες. Έτσι, αν V κυβικές μονάδες είναι ο όγκος του ορθού κυκλικού κυλίνδρου, από τα αθροίσματα Riemann,
V o l u m e o f c y l i n d e r = lim | | | Δ → |0 | ∑ i = n 1A ( w i ) Δ i x {\displaystyle \mathrm {Volume\;of\;cylinder} =\lim _{||\Delta \to 0|||}\sum _{i=1}^{n}A(w_{i})\Delta _{i}x}
= ∫ h0 A ( y ) d2 y {\displaystyle =\int _{0}^{h}A(y)^{2}\,dy}
= ∫ h0 π r d2 y {\displaystyle =\int _{0}^{h}\pi r^{2}\,dy}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Χρησιμοποιώντας κυλινδρικές συντεταγμένες, ο όγκος μπορεί να υπολογιστεί με ολοκλήρωση επί
= ∫ h0 ∫ π02 ∫ r0 s d s d ϕ d z {\displaystyle =\int _{0}^{h}\int _{0}^{2\pi }\int _{0}^{r}s\,\,ds\,d\phi \,dz}
= π r h 2{\displaystyle =\pi \,r^{2}\,h\,}
Κυλινδρική τομή
Οι κυλινδρικές τομές είναι οι τομές των κυλίνδρων με τα επίπεδα. Για έναν ορθό κυκλικό κύλινδρο, υπάρχουν τέσσερις δυνατότητες. Ένα επίπεδο εφαπτόμενο στον κύλινδρο, συναντά τον κύλινδρο σε μια απλή ευθεία γραμμή. Κινούμενο ενώ είναι παράλληλο με τον εαυτό του, το επίπεδο είτε δεν τέμνει τον κύλινδρο είτε τον τέμνει σε δύο παράλληλες ευθείες. Όλα τα άλλα επίπεδα τέμνουν τον κύλινδρο σε έλλειψη ή, όταν είναι κάθετα στον άξονα του κυλίνδρου, σε κύκλο.
Άλλοι τύποι κυλίνδρων
Ένας ελλειπτικός κύλινδρος, ή κυλινδροειδές, είναι μια τετραγωνική επιφάνεια, με την ακόλουθη εξίσωση σε καρτεσιανές συντεταγμένες:
( x a ) +2 ( y b ) =21 . {\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=1.}
Αυτή η εξίσωση αφορά έναν ελλειπτικό κύλινδρο, μια γενίκευση του συνηθισμένου, κυκλικού κυλίνδρου (a = b). Ακόμη πιο γενικευμένος είναι ο γενικευμένος κύλινδρος: η διατομή μπορεί να είναι οποιαδήποτε καμπύλη.
Ο κύλινδρος είναι ένα εκφυλισμένο τετράγωνο επειδή τουλάχιστον μία από τις συντεταγμένες (στην περίπτωση αυτή η z) δεν εμφανίζεται στην εξίσωση.
Σε έναν λοξό κύλινδρο η άνω και η κάτω επιφάνεια είναι μετατοπισμένες η μία από την άλλη.
Υπάρχουν και άλλοι πιο ασυνήθιστοι τύποι κυλίνδρων. Αυτοί είναι οι φανταστικοί ελλειπτικοί κύλινδροι:
( x a ) +2 ( y b ) = 2- 1{\displaystyle \left({\frac {x}{a}}}\right)^{2}+\left({\frac {y}{b}}}\right)^{2}=-1}
ο υπερβολικός κύλινδρος:
( x a ) 2- ( y b ) = 2{\displaystyle1 \left({\frac {x}{a}}}\right)^{2}-\left({\frac {y}{b}}}\right)^{2}=1}
και τον παραβολικό κύλινδρο:
x +2 a2 y =0 . {\displaystyle x^{2}+2ay=0.\,}

Ένας ελλειπτικός κύλινδρος

Στην προβολική γεωμετρία, ένας κύλινδρος είναι απλώς ένας κώνος του οποίου η κορυφή βρίσκεται στο άπειρο, πράγμα που αντιστοιχεί οπτικά σε έναν κύλινδρο που στην προοπτική εμφανίζεται ως κώνος προς τον ουρανό.
Προβολική γεωμετρία
Στην προβολική γεωμετρία, ένας κύλινδρος είναι απλώς ένας κώνος του οποίου η κορυφή βρίσκεται στο άπειρο.
Αυτό είναι χρήσιμο στον ορισμό των εκφυλισμένων κωνικών, που απαιτούν την εξέταση των κυλινδρικών κωνικών.
Ερωτήσεις και απαντήσεις
Ε: Τι είναι ο κύλινδρος;
A: Ο κύλινδρος είναι ένα τρισδιάστατο γεωμετρικό σχήμα με την επιφάνεια να σχηματίζεται από σημεία σε σταθερή απόσταση από ένα δεδομένο ευθύγραμμο τμήμα, γνωστό ως άξονας του κυλίνδρου. Μπορεί να θεωρηθεί ως ένα κυκλικό πρίσμα και τόσο η επιφάνεια όσο και το στερεό σχήμα που δημιουργείται στο εσωτερικό του μπορούν να ονομαστούν κύλινδρος.
Ερ: Πόσο καιρό οι άνθρωποι γνωρίζουν για την επιφάνεια και τον όγκο των κυλίνδρων;
Α: Το εμβαδόν επιφάνειας και ο όγκος των κυλίνδρων είναι γνωστά από την αρχαιότητα.
Ερ: Τι είναι ο ελλειπτικός, ο παραβολικός και ο υπερβολικός κύλινδρος;
Α: Οι ελλειπτικοί, παραβολικοί και υπερβολικοί κύλινδροι είναι κύλινδροι των οποίων η διατομή είναι έλλειψη, παραβολή ή υπερβολή αντίστοιχα.
Ερ: Πώς ορίζεται ένας κύλινδρος στη διαφορική γεωμετρία;
Α: Στη διαφορική γεωμετρία, ένας κύλινδρος ορίζεται ευρύτερα ως μια κυβερνημένη επιφάνεια η οποία καλύπτεται από μια μονοπαραμετρική οικογένεια παράλληλων ευθειών.
Ερ: Τι σημαίνει ότι κάτι είναι "κυβερνημένο";
Α: Το να είναι "κυβερνημένη" σημαίνει ότι έχει ευθείες γραμμές σχεδιασμένες πάνω του με τον ένα ή τον άλλο τρόπο.
Ερ: Υπάρχει μόνο ένας τύπος κυλίνδρου;
Α: Όχι, υπάρχουν πολλοί διαφορετικοί τύποι κυλίνδρων, όπως οι ελλειπτικοί, οι παραβολικοί και οι υπερβολικοί κύλινδροι, οι οποίοι έχουν διαφορετικές διατομές.
ψάχνω










