Ρολόι του φωτός

Το ρολόι του φωτός είναι ένας απλός τρόπος για να δείξουμε ένα βασικό χαρακτηριστικό της Ειδικής Σχετικότητας. Ένα ρολόι είναι σχεδιασμένο να λειτουργεί με την ανάκλαση μιας λάμψης φωτός από έναν μακρινό καθρέφτη και τη χρησιμοποίηση της επιστροφής της για να ενεργοποιήσει μια άλλη λάμψη φωτός, μετρώντας εν τω μεταξύ πόσες λάμψεις έχουν εμφανιστεί στη διαδρομή. Είναι εύκολο να δείξουμε ότι οι άνθρωποι στη Γη που παρακολουθούν ένα διαστημόπλοιο να πετάει από πάνω μας με ένα τέτοιο ρολόι θα το έβλεπαν να χτυπάει σχετικά αργά. Το φαινόμενο αυτό ονομάζεται διαστολήτου χρόνου.

Πριν μελετήσουμε το ρολόι του φωτός, εξετάστε ένα άλλο είδος σχετικότητας. Φανταστείτε ότι κάποιος ντριμπλάρει μια μπάλα μπάσκετ στο αμπάρι ενός μεγάλου αεροσκάφους μεταφοράς φορτίου. Ο μπασκετμπολίστας κινείται προς την ίδια κατεύθυνση με το τζετ του αεροπλάνου. Οι άλλοι άνθρωποι στο αεροπλάνο τον βλέπουν να κινείται ένα ή δύο μέτρα καθώς κάνει μια ντρίμπλα. Μεταξύ της στιγμής που η μπάλα αναπηδά την πρώτη φορά και της στιγμής που η μπάλα αναπηδά τη δεύτερη φορά, έχει περάσει περίπου ένα δευτερόλεπτο. Αλλά όταν έγινε η πρώτη αναπήδηση η μπάλα του μπάσκετ βρισκόταν πάνω από το Γιβραλτάρ και όταν έγινε η δεύτερη αναπήδηση η μπάλα του μπάσκετ βρισκόταν πάνω από το νερό πιο κοντά στην Ισπανία. Έτσι, η μπάλα του μπάσκετ έχει μετακινηθεί 280 μέτρα σε σχέση με τη Γη.

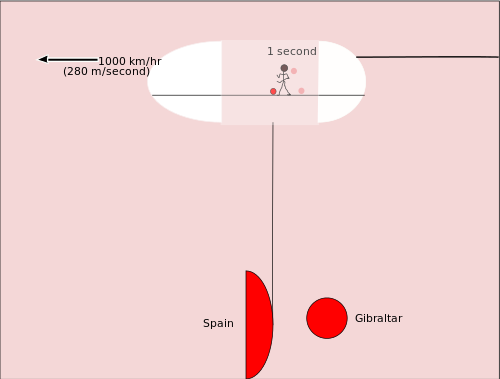
Τώρα εξετάστε ένα κάπως παρόμοιο ζήτημα σχετικής κίνησης. Αυτή τη φορά θα εξετάσουμε τι βλέπουν οι άνθρωποι που κοιτάζουν τα αστέρια από το Βόρειο Πόλο όταν ένα πολύ γρήγορο διαστημόπλοιο πετάει από πάνω τους. Μπορούμε να χρησιμοποιήσουμε την άλγεβρα και το Πυθαγόρειο θεώρημα για να υπολογίσουμε πόσο επιβραδύνεται ο χρόνος στο διαστημόπλοιο. Το μόνο άλλο πράγμα που χρειαζόμαστε είναι η εξίσωση που συνδέει την απόσταση, d, τον ρυθμό ή την ταχύτητα του ταξιδιού, r, και τον χρόνο, t. Η εξίσωση είναι:

d = rt

Η ταχύτητα του φωτός είναι σταθερή, οπότε θα εφαρμόσουμε αυτή την τιμή σε δύο προβλήματα. Θα ονομάσουμε την ταχύτητα του φωτός c, καθώς αυτό είναι το γράμμα που χρησιμοποιούν συνήθως οι επιστήμονες για να την ονομάσουν.

Ένα ρολόι κατασκευάζεται τοποθετώντας μια έξοδο φωτός στο κάτω μέρος ενός μακρύ στύλου, έναν καθρέφτη στην κορυφή του στύλου και έναν ηλεκτρονικό ανιχνευτή φωτός στο κάτω μέρος του στύλου. Το ρολόι εκκινείται με το σύντομο κλείσιμο ενός διακόπτη που στέλνει μια αναλαμπή φωτός από το κάτω μέρος του στύλου στην κορυφή του στύλου όπου αντανακλάται πίσω στο κάτω μέρος του στύλου. Όταν ο ανιχνευτής φωτός στο κάτω μέρος του στύλου δει το ανοιγόκλεισμα του φωτός, κάνει δύο πράγματα. Προσθέτει ένα στον μετρητή που είναι συνδεδεμένος με αυτόν και εκτοξεύει άλλο ένα φως που αναβοσβήνει προς τον καθρέφτη. Όταν αυτό το ανοιγόκλεισμα του φωτός φτάσει πίσω στο κάτω μέρος, ο μετρητής αλλάζει σε δύο και ενεργοποιείται άλλο ένα ανοιγόκλεισμα του φωτός. Δεδομένου ότι το φως ταξιδεύει πολύ γρήγορα (300.000 χιλιόμετρα/δευτερόλεπτο), για κάθε δευτερόλεπτο που μετράται από ένα συνηθισμένο ρολόι, το ρολόι του φωτός θα "χτυπάει" έναν πολύ μεγάλο αριθμό φορών.

Για να διευκολύνουμε τα μαθηματικά, θα πούμε ότι ο στύλος έχει μήκος μισό χιλιόμετρο. Έτσι, αν στεκόμαστε δίπλα στο φωτεινό ρολόι που είναι χτισμένο δίπλα στο μεγάλο τηλεσκόπιο στο Βόρειο Πόλο, θα δούμε ότι το φως διανύει ένα χιλιόμετρο για κάθε "τικ" του φωτεινού ρολογιού. Δεδομένου ότι η απόσταση που διανύει, d, ισούται με την ταχύτητα επί το χρόνο και η ταχύτητα που εμπλέκεται είναι c, έχουμε την εξίσωση:

d = ct

και μπορούμε να λύσουμε αυτή την εξίσωση για το t για να μάθουμε πόσο διαρκεί σε δευτερόλεπτα κάθε "τικ".

1 χλμ = 300.000 χλμ/δευτερόλεπτο * t δευτερόλεπτα

t δευτερόλεπτα = 1 km/300,000 (km/δευτερόλεπτο) = 1/300,000 δευτερόλεπτα = 0.00000333...3 δευτερόλεπτα

Με άλλα λόγια, κάθε "χτύπημα" του ρολογιού του φωτός θα διαρκεί 0,00000333...3 δευτερόλεπτα.

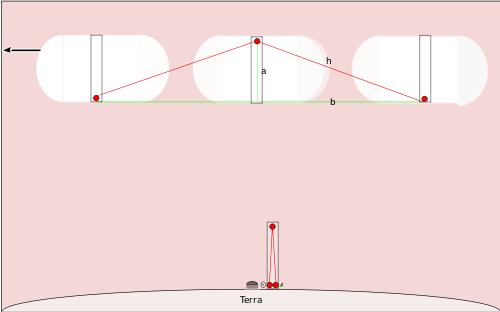
Αν ένα διαστημόπλοιο πετούσε σε μια ευθεία γραμμή περνώντας πάνω από το Βόρειο Πόλο με ένα μεγάλο κλάσμα της ταχύτητας του φωτός, και είχε ένα παρόμοιο ρολόι, οι άνθρωποι που παρακολουθούσαν το πέρασμά του θα έβλεπαν ότι το κάτοπτρο στην κορυφή του πόλου είχε μετακινηθεί από ακριβώς πάνω από το φως που εκπέμπει, οπότε το φως θα ταξίδευε κατά μήκος της γραμμής που σημειώνεται με h στο διάγραμμα, και στη συνέχεια θα ακολουθούσε την άλλη υποτείνουσα πίσω στη βάση του πόλου - η οποία θα είχε πλέον μετακινηθεί σε κάποια απόσταση, αφού το διαστημόπλοιο κινείται τόσο γρήγορα. Μπορούμε να υπολογίσουμε πόσο χρόνο θα χρειαζόταν ένα τικ σύμφωνα με τους ανθρώπους στη Γη. Ξέρουμε ότι ο πόλος του διαστημοπλοίου έχει μήκος α, αφού είναι το ίδιο είδος ρολογιού που χρησιμοποιούν οι άνθρωποι στο Βόρειο Πόλο. Θέλουμε να υπολογίσουμε το t' , το χρόνο που χρειάζεται για να κάνει ένα τικ το ρολόι στο διαστημόπλοιο.

Γνωρίζουμε ότι το διαστημόπλοιο θα ταξιδέψει 1/2 r t' ενώ η αναλαμπή του φωτός κατευθύνεται προς τα πάνω προς το κάτοπτρο, και άλλο 1/2 r t' ενώ η αναλαμπή του φωτός κατευθύνεται προς τα κάτω προς τη βάση του πόλου. Έτσι, αυτός ο υπολογισμός μας δίνει το μήκος της γραμμής b στο διάγραμμα. Γνωρίζουμε το a, οπότε μπορούμε να υπολογίσουμε το h με το Πυθαγόρειο θεώρημα:

h = √(a2 + (rt' /2)²)

Έτσι, η συνολική απόσταση που διανύει το φως είναι 2 h ή d = 2 √(a2 + (rt' /2)²)

Γνωρίζουμε επίσης ότι η ταχύτητα του φωτός, c, είναι σταθερή. Όποιος κι αν την μετρήσει, αποδεικνύεται ότι είναι η ίδια ταχύτητα. Έτσι μπορούμε να χρησιμοποιήσουμε αυτό το γεγονός για να βρούμε έναν άλλο τρόπο υπολογισμού του χρόνου που χρειάζεται η λάμψη του φωτός για να πάει από τη βάση στην κορυφή του πόλου και πάλι πίσω:

t' = d/c

Με άλλα λόγια, d = c t' .

Έτσι μπορούμε να γράψουμε

c t' = 2 √(a2 + (rt' /2)²)

ή

1/2 c t' = √(a2 + (rt' /2)²)

Για να λύσουμε την παραπάνω εξίσωση, θα πρέπει να:

1. Τετράγωνο και στις δύο πλευρές
2. Διαιρέστε και τις δύο πλευρές με t' ²
3. Πολλαπλασιάστε και τις δύο πλευρές επί 4
4. Διαιρέστε και τις δύο πλευρές με c2
5. Απλοποιήστε c2 / c2
6. Αφαιρέστε r2/c2 και από τις δύο πλευρές
7. Πάρτε την τετραγωνική ρίζα και των δύο πλευρών
8. Πολλαπλασιάστε και τις δύο πλευρές με t'
9. Διαιρέστε και τις δύο πλευρές με √(1-r2/c2)

Λύνοντας την παραπάνω εξίσωση βρίσκουμε ότι:

t' = 2a/(c√(1-r2/c2)

Ο χρόνος μεταξύ των χτύπων του ρολογιού στο Βόρειο Πόλο είναι 2a/c, οπότε μπορούμε να γράψουμε:

t' = t/√(1-r2/c2)

Αν t = 1 δευτερόλεπτο, τότε αν το διαστημόπλοιο ταξιδεύει με το μισό της ταχύτητας του φωτός, t' = 1,1547 δευτερόλεπτα.

Πειραματιστείτε με διάφορες ταχύτητες ταξιδιού σε: http://www.1728.org/reltivty.htm

Ερωτήσεις και απαντήσεις

Q: Τι είναι το φωτεινό κουδούνι;

Q: Τι είναι η διαστολή του χρόνου;

Ερ: Πώς μπορούμε να υπολογίσουμε πόσο επιβραδύνεται ο χρόνος σε ένα διαστημόπλοιο;

Q: Πώς λειτουργεί ένα ρολόι με φως;

Ερ: Ποια εξίσωση χρειαζόμαστε για αυτόν τον υπολογισμό;

Ε. Πώς σχετίζεται το θεώρημα του Πυθαγόρα με αυτόν τον υπολογισμό;

Αναζήτηση με γράμμα