Άλγεβρα

Ιστορία

Οι πρώτες μορφές της άλγεβρας αναπτύχθηκαν από τους Βαβυλώνιους και τους Έλληνες γεωμέτρες, όπως ο Ήρωας της Αλεξάνδρειας. Ωστόσο, η λέξη "άλγεβρα" είναι λατινική μορφή της αραβικής λέξης Al-Jabr ("χύτευση") και προέρχεται από το βιβλίο μαθηματικών Al-Maqala fi Hisab-al Jabr wa-al-Muqabilah, ("Δοκίμιο για τον υπολογισμό της χύτευσης και της εξίσωσης") που γράφτηκε τον 9ο αιώνα από έναν Πέρση μαθηματικό, τον Muhammad ibn Mūsā al-Khwārizmī, ο οποίος ήταν μουσουλμάνος που γεννήθηκε στο Khwarizm του Ουζμπεκιστάν. Άκμασε υπό τον Αλ-Μα'μουν στη Βαγδάτη του Ιράκ κατά τα έτη 813-833 μ.Χ. και πέθανε γύρω στο 840 μ.Χ. Το βιβλίο μεταφέρθηκε στην Ευρώπη και μεταφράστηκε στα λατινικά τον 12ο αιώνα. Το βιβλίο πήρε τότε το όνομα "Άλγεβρα". (Η κατάληξη του ονόματος του μαθηματικού, al-Khwarizmi, άλλαξε σε μια λέξη που ήταν ευκολότερο να ειπωθεί στα λατινικά, και έγινε η αγγλική λέξη algorithm).

Παραδείγματα

Ακολουθεί ένα απλό παράδειγμα προβλήματος άλγεβρας:

Η Sue έχει 12 καραμέλες και η Ann έχει 24 καραμέλες. Αποφασίζουν να μοιραστούν, ώστε να έχουν τον ίδιο αριθμό καραμελών. Πόσες καραμέλες θα έχει η καθεμία;

Αυτά είναι τα βήματα που μπορείτε να χρησιμοποιήσετε για να λύσετε το πρόβλημα:

1. Για να έχει τον ίδιο αριθμό καραμελών, η Ann πρέπει να δώσει μερικές στη Sue. Έστω x ο αριθμός των καραμελών που δίνει η Ann στη Sue.
2. Οι καραμέλες της Sue, συν x, πρέπει να είναι ίδιες με τις καραμέλες της Ann μείον x. Αυτό γράφεται ως εξής: 12 + x = 24 - x
3. Αφαιρέστε το 12 και από τις δύο πλευρές της εξίσωσης. Αυτό δίνει: x = 12 - x. (Ό,τι συμβαίνει στη μία πλευρά του σημείου της ισότητας πρέπει να συμβεί και στην άλλη πλευρά, για να εξακολουθεί να ισχύει η εξίσωση. Έτσι, σε αυτή την περίπτωση, όταν το 12 αφαιρέθηκε και από τις δύο πλευρές, υπήρξε ένα μεσαίο βήμα 12 + x - 12 = 24 - x - 12. Αφού ένα άτομο αισθάνεται άνετα με αυτό, το μεσαίο βήμα δεν γράφεται).
4. Προσθέστε το x και στις δύο πλευρές της εξίσωσης. Αυτό δίνει: 2x = 12
5. Διαιρέστε και τις δύο πλευρές της εξίσωσης με το 2. Αυτό δίνει x = 6. Η απάντηση είναι έξι. Αν η Ann δώσει στη Sue 6 καραμέλες, θα έχουν τον ίδιο αριθμό καραμελών.
6. Για να το ελέγξετε αυτό, βάλτε το 6 πίσω στην αρχική εξίσωση, όπου το x ήταν: 12 + 6 = 24 - 6
7. Αυτό δίνει 18=18, το οποίο είναι αληθές. Ο καθένας τους έχει τώρα 18 καραμέλες.

Με εξάσκηση, η άλγεβρα μπορεί να χρησιμοποιηθεί όταν αντιμετωπίζετε ένα πρόβλημα που είναι πολύ δύσκολο να λυθεί με οποιονδήποτε άλλο τρόπο. Προβλήματα όπως η κατασκευή ενός αυτοκινητόδρομου, ο σχεδιασμός ενός κινητού τηλεφώνου ή η εύρεση της θεραπείας για μια ασθένεια απαιτούν άλγεβρα.

Γράφοντας άλγεβρα

Όπως στα περισσότερα μέρη των μαθηματικών, η πρόσθεση του z στο y (ή y συν z) γράφεται ως y + z. Η αφαίρεση του z από το y (ή y μείον z) γράφεται ως y - z. Η διαίρεση του y με το z (ή y πάνω από το z: y z {\displaystyle y \over z} ) γράφεται ως y ÷ z ή y/z. Το y/z χρησιμοποιείται πιο συχνά.

Στην άλγεβρα, ο πολλαπλασιασμός y επί z (ή y επί z) μπορεί να γραφτεί με 4 τρόπους: y × z, y * z, y-z, ή απλά yz. Το σύμβολο πολλαπλασιασμού "×" συνήθως δεν χρησιμοποιείται, επειδή μοιάζει πολύ με το γράμμα x, το οποίο χρησιμοποιείται συχνά ως μεταβλητή. Επίσης, κατά τον πολλαπλασιασμό μιας μεγαλύτερης έκφρασης, μπορούν να χρησιμοποιηθούν παρενθέσεις: y (z+1).

Όταν πολλαπλασιάζουμε έναν αριθμό και ένα γράμμα στην άλγεβρα, γράφουμε τον αριθμό μπροστά από το γράμμα: 5 × y = 5y. Όταν ο αριθμός είναι το 1, τότε το 1 δεν γράφεται, επειδή 1 επί οποιονδήποτε αριθμό είναι αυτός ο αριθμός (1 × y = y) και έτσι δεν χρειάζεται.

Παρεμπιπτόντως, δεν χρειάζεται να χρησιμοποιείτε τα γράμματα x ή y στην άλγεβρα. Οι μεταβλητές είναι απλά σύμβολα που σημαίνουν κάποιον άγνωστο αριθμό ή τιμή, οπότε μπορείτε να χρησιμοποιήσετε οποιαδήποτε μεταβλητή. x και y είναι τα πιο συνηθισμένα, όμως.

Συναρτήσεις και γραφικές παραστάσεις

Ένα σημαντικό μέρος της άλγεβρας είναι η μελέτη των συναρτήσεων, καθώς οι συναρτήσεις εμφανίζονται συχνά σε εξισώσεις που προσπαθούμε να λύσουμε. Μια συνάρτηση είναι σαν μια μηχανή στην οποία μπορείτε να βάλετε έναν αριθμό (ή αριθμούς) και να πάρετε έναν συγκεκριμένο αριθμό (ή αριθμούς). Όταν χρησιμοποιούμε συναρτήσεις, οι γραφικές παραστάσεις μπορούν να αποτελέσουν ισχυρά εργαλεία που μας βοηθούν να μελετήσουμε τις λύσεις των εξισώσεων.

Η γραφική παράσταση είναι μια εικόνα που δείχνει όλες τις τιμές των μεταβλητών που καθιστούν την εξίσωση ή την ανισότητα αληθή. Συνήθως αυτό είναι εύκολο να γίνει όταν υπάρχουν μόνο μία ή δύο μεταβλητές. Η γραφική παράσταση είναι συχνά μια γραμμή και αν η γραμμή δεν καμπυλώνει ή δεν πηγαίνει ευθεία πάνω-κάτω μπορεί να περιγραφεί από τον βασικό τύπο y = mx + b. Η μεταβλητή b είναι η y-κορυφή της γραφικής παράστασης (όπου η γραμμή τέμνει τον κατακόρυφο άξονα) και m είναι η κλίση ή η απότομη κλίση της γραμμής. Ο τύπος αυτός ισχύει για τις συντεταγμένες μιας γραφικής παράστασης, όπου κάθε σημείο της ευθείας γράφεται (x, y).

Σε ορισμένα μαθηματικά προβλήματα, όπως η εξίσωση μιας ευθείας, μπορεί να υπάρχουν περισσότερες από μία μεταβλητές (x και y σε αυτή την περίπτωση). Για να βρεθούν τα σημεία της ευθείας, αλλάζει η μία μεταβλητή. Η μεταβλητή που αλλάζει ονομάζεται "ανεξάρτητη" μεταβλητή. Στη συνέχεια γίνονται μαθηματικές πράξεις για να προκύψει ένας αριθμός. Ο αριθμός που προκύπτει ονομάζεται "εξαρτημένη" μεταβλητή. Τις περισσότερες φορές η ανεξάρτητη μεταβλητή γράφεται ως x και η εξαρτημένη μεταβλητή γράφεται ως y, για παράδειγμα, στο y = 3x + 1. Αυτό συχνά τοποθετείται σε μια γραφική παράσταση, χρησιμοποιώντας έναν άξονα x (που πηγαίνει αριστερά και δεξιά) και έναν άξονα y (που πηγαίνει πάνω και κάτω). Μπορεί επίσης να γραφτεί σε μορφή συνάρτησης: f(x) = 3x + 1. Έτσι, σε αυτό το παράδειγμα, θα μπορούσαμε να βάλουμε 5 για το x και να πάρουμε y = 16. Αν βάζαμε 2 για το x θα παίρναμε y=7. Και το 0 για το x θα έπαιρνε y=1. Έτσι, θα υπήρχε μια ευθεία που θα περνούσε από τα σημεία (5,16), (2,7) και (0,1), όπως φαίνεται στη γραφική παράσταση στα δεξιά.

Αν το x έχει δύναμη 1, είναι ευθεία γραμμή. Αν είναι τετραγωνική ή κάποια άλλη δύναμη, θα είναι καμπύλη. Αν χρησιμοποιεί μια ανισότητα (< ή > ), τότε συνήθως ένα μέρος της γραφικής παράστασης σκιάζεται, είτε πάνω είτε κάτω από την ευθεία.

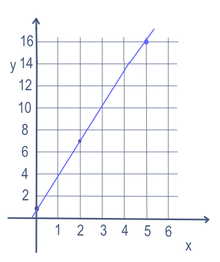
Γραμμική εξίσωση για y=3x+1

Κανόνες της άλγεβρας

Στην άλγεβρα, υπάρχουν μερικοί κανόνες που μπορούν να χρησιμοποιηθούν για την περαιτέρω κατανόηση των εξισώσεων. Αυτοί ονομάζονται κανόνες της άλγεβρας. Ενώ αυτοί οι κανόνες μπορεί να φαίνονται παράλογοι ή προφανείς, είναι φρόνιμο να κατανοήσετε ότι αυτές οι ιδιότητες δεν ισχύουν σε όλους τους κλάδους των μαθηματικών. Ως εκ τούτου, θα ήταν χρήσιμο να γνωρίζουμε πώς δηλώνονται αυτοί οι αξιωματικοί κανόνες, πριν τους θεωρήσουμε δεδομένους. Πριν προχωρήσετε στους κανόνες, σκεφτείτε δύο ορισμούς που θα δοθούν.

1. Το αντίθετο - το αντίθετο του {\displaystyle a} είναι - ένα {\displaystyle -a} .
2. Αντίστροφο - το αντίστροφο του a {\displaystyle a} είναι 1 a {\displaystyle {\frac {1}{a}}} .

Κανόνες

Η αντιμεταθετική ιδιότητα της πρόσθεσης

'Commutative' σημαίνει ότι μια συνάρτηση έχει το ίδιο αποτέλεσμα αν οι αριθμοί αντικατασταθούν. Με άλλα λόγια, η σειρά των όρων σε μια εξίσωση δεν έχει σημασία. Όταν ο τελεστής δύο όρων είναι μια πρόσθεση, ισχύει η "αντιμεταθετική ιδιότητα της πρόσθεσης". Σε αλγεβρικούς όρους, αυτό δίνει a + b = b + a {\displaystyle a+b=b+a} .

Σημειώστε ότι αυτό δεν ισχύει για την αφαίρεση! (δηλ. a - b ≠ b - a {\displaystyle a-b\neq b-a} )

Commutative ιδιότητα του πολλαπλασιασμού

Όταν ο τελεστής δύο όρων είναι ένας πολλαπλασιασμός, εφαρμόζεται η "αντιμεταθετική ιδιότητα του πολλαπλασιασμού". Σε αλγεβρικούς όρους, αυτό δίνει a ⋅ b = b ⋅ a {\displaystyle a\cdot b=b\cdot a} .

Σημειώστε ότι αυτό δεν ισχύει για τη διαίρεση! (δηλ. a b ≠ b a {\displaystyle {\frac {a}{b}}\neq {\frac {b}{a}}} , όταν a ≠ b {\displaystyle a\neq b} )

Συσχετιστική ιδιότητα της πρόσθεσης

Ο όρος "συσχετισμός" αναφέρεται στην ομαδοποίηση των αριθμών. Η συνειρμική ιδιότητα της πρόσθεσης συνεπάγεται ότι, όταν προστίθενται τρεις ή περισσότεροι όροι, δεν έχει σημασία πώς ομαδοποιούνται αυτοί οι όροι. Αλγεβρικά, αυτό δίνει a + ( b + c ) = ( a + b ) + c {\displaystyle a+(b+c)=(a+b)+c} . Σημειώστε ότι αυτό δεν ισχύει για την αφαίρεση, π.χ. 1 = 0 - ( 0 - 1 ) ≠ ( 0 - 0 ) - 1 = - 1 {\displaystyle 1=0-(0-1)\neq (0-0)-1=-1} (βλέπε διανεμητική ιδιότητα).

Συσχετιστική ιδιότητα του πολλαπλασιασμού

Η συνειρμική ιδιότητα του πολλαπλασιασμού συνεπάγεται ότι, όταν πολλαπλασιάζουμε τρεις ή περισσότερους όρους, δεν έχει σημασία πώς αυτοί οι όροι ομαδοποιούνται. Αλγεβρικά, αυτό δίνει a ⋅ ( b ⋅ c ) = ( a ⋅ b ) ⋅ c {\displaystyle a\cdot (b\cdot c)=(a\cdot b)\cdot c} . Σημειώστε ότι αυτό δεν ισχύει για τη διαίρεση, π.χ. 2 = 1 / ( 1 / 2 ) ≠ ( 1 / 1 ) / 2 = 1 / 2 {\displaystyle 2=1/(1/2)\neq (1/1)/2=1/2} .

Διανεμητική ιδιότητα

Η διανεμητική ιδιότητα δηλώνει ότι ο πολλαπλασιασμός ενός αριθμού με έναν άλλο όρο μπορεί να διανεμηθεί. Για παράδειγμα: a ⋅ ( b + c ) = a b + a c {\displaystyle a\cdot (b+c)=ab+ac} . (Μην το μπερδεύετε αυτό με τις συσχετιστικές ιδιότητες! Για παράδειγμα, a ⋅ ( b + c ) ≠ ( a ⋅ b ) + c {\displaystyle a\cdot (b+c)\neq (a\cdot b)+c} .)

Προσθετική ιδιότητα ταυτότητας

Η "ταυτότητα" αναφέρεται στην ιδιότητα ενός αριθμού να είναι ίσος με τον εαυτό του. Με άλλα λόγια, υπάρχει μια πράξη δύο αριθμών έτσι ώστε να ισούται με τη μεταβλητή του αθροίσματος. Η προσθετική ιδιότητα της ταυτότητας δηλώνει ότι το άθροισμα οποιουδήποτε αριθμού και του 0 είναι αυτός ο αριθμός: a + 0 = a {\displaystyle a+0=a} . Αυτό ισχύει και για την αφαίρεση: a - 0 = a {\displaystyle a-0=a} .

Ιδιότητα πολλαπλασιαστικής ταυτότητας

Η πολλαπλασιαστική ιδιότητα ταυτότητας δηλώνει ότι το γινόμενο οποιουδήποτε αριθμού και του 1 είναι ο αριθμός αυτός: a ⋅ 1 = a {\displaystyle a\cdot 1=a} . Αυτό ισχύει και για τη διαίρεση: a 1 = a {\displaystyle {\frac {a}{1}}=a} .

Προσθετική αντίστροφη ιδιότητα

Η προσθετική αντίστροφη ιδιότητα είναι κάτι σαν το αντίθετο της προσθετικής ταυτότητας. Όταν μια πράξη είναι το άθροισμα ενός αριθμού και του αντιθέτου του και ισούται με 0, η πράξη αυτή είναι μια έγκυρη αλγεβρική πράξη. Αλγεβρικά, δηλώνει το εξής: a - a = 0 {\displaystyle a-a=0} . Το προσθετικό αντίστροφο του 1 είναι το (-1).

Πολλαπλασιαστική αντίστροφη ιδιότητα

Η πολλαπλασιαστική αντίστροφη ιδιότητα συνεπάγεται ότι όταν μια πράξη είναι το γινόμενο ενός αριθμού και του αντιστρόφου του και ισούται με 1, η πράξη αυτή είναι έγκυρη αλγεβρική πράξη. Αλγεβρικά, δηλώνει τα εξής: a a = 1 {\displaystyle {\frac {a}{a}}=1} . Το πολλαπλασιαστικό αντίστροφο του 2 είναι 1/2.

Προχωρημένη Άλγεβρα

Εκτός από τη "στοιχειώδη άλγεβρα", ή βασική άλγεβρα, υπάρχουν προχωρημένες μορφές άλγεβρας, που διδάσκονται στα κολέγια και τα πανεπιστήμια, όπως η αφηρημένη άλγεβρα, η γραμμική άλγεβρα και η καθολική άλγεβρα. Αυτό περιλαμβάνει τον τρόπο χρήσης ενός πίνακα για την επίλυση πολλών γραμμικών εξισώσεων ταυτόχρονα. Η αφηρημένη άλγεβρα είναι η μελέτη των πραγμάτων που βρίσκονται σε εξισώσεις, πηγαίνοντας πέρα από τους αριθμούς στο πιο αφηρημένο με ομάδες αριθμών.

Πολλά μαθηματικά προβλήματα αφορούν τη φυσική και τη μηχανική. Σε πολλά από αυτά τα προβλήματα φυσικής ο χρόνος είναι μια μεταβλητή. Ο χρόνος χρησιμοποιεί το γράμμα t. Η χρήση των βασικών ιδεών της άλγεβρας μπορεί να βοηθήσει στη μείωση ενός μαθηματικού προβλήματος στην απλούστερη μορφή του, διευκολύνοντας την επίλυση δύσκολων προβλημάτων. Η ενέργεια είναι e, η δύναμη είναι f, η μάζα είναι m, η επιτάχυνση είναι a και η ταχύτητα του φωτός είναι μερικές φορές c. Αυτό χρησιμοποιείται σε μερικές διάσημες εξισώσεις, όπως f = ma και e=mc^2 (αν και χρειάστηκαν πιο πολύπλοκα μαθηματικά πέρα από την άλγεβρα για να βγει αυτή η τελευταία εξίσωση).

Σχετικές σελίδες

• Κατάλογος μαθηματικών θεμάτων
• Σειρά επιχειρήσεων
• Παραβολή
• Σύστημα Άλγεβρας Υπολογιστών