Αρχή της απροσδιοριστίας

Διαγράμματα

6. Αυτό το κινούμενο σχέδιο δείχνει μια από τις σημαντικές συνέπειες της αβεβαιότητας του σύμπαντος: την κβαντική σήραγγα των ηλεκτρονίων. Κοιτάξτε προσεκτικά. Κάθε φορά ένα μικρό κομμάτι περνάει μέσα από το φράγμα.


5. Η ανάρτηση του κεντρικού διακένου με ζυγαριά ελατηρίου επιτρέπει τη μέτρηση της ορμής, αλλά με αυτόν τον τρόπο το διάκενο μετακινείται απρόβλεπτα, οπότε χάνεται η πληροφορία για τη θέση κάθε φωτονίου στο κέντρο.


4. Η τοποθέτηση ελατηρίου σε ένα φράγμα με μια μικρή οπή κάνει το σωματίδιο να πιέζεται μέσα από την οπή, γεγονός που ωθεί το φράγμα, τεντώνει τα ελατήρια και έτσι μετράει την ορμή. Επειδή όμως το εμπόδιο που είναι τοποθετημένο με ελατήριο κινείται, δεν είμαστε τόσο σίγουροι για το πού βρισκόταν το σωματίδιο όταν πέρασε από την οπή, και η περίθλαση θα επηρεάσει επίσης τη θέση του στην οθόνη ανίχνευσης.


3. Στενεύοντας την οπή αυξάνεται η βεβαιότητα για το πού βρίσκεται το φωτόνιο στη μέση, αλλά στη συνέχεια η κατεύθυνσή του από εκεί προς την οθόνη ανίχνευσης στα δεξιά γίνεται αντίστοιχα πιο αβέβαιη. Η εστίαση γίνεται θολή. Η διεύρυνση της οπής κάνει τα φωτόνια να καταλήγουν όλα στο κέντρο της οθόνης ανίχνευσης, αλλά τότε έχουμε λιγότερη ιδέα για το πού βρίσκονταν όταν πέρασαν από το κεντρικό φράγμα.


1. Τα φωτόνια, τα ηλεκτρόνια και άλλα υποατομικά σωματίδια θα έρθουν σε ευκρινή εστίαση όταν πυροβοληθούν μέσα από μια μεγάλη τρύπα, αλλά δεν γνωρίζουμε ακριβώς πού βρίσκονταν στη μέση της διαδρομής τους.


2. Το στένεμα της οπής κάμπτει τις διαδρομές των σωματιδίων γύρω από τις άκρες της οπής (περίθλαση), οπότε η προκύπτουσα δέσμη γίνεται μεγαλύτερη και πιο μαλακή.

Πώς έμαθαν οι άνθρωποι για την αβεβαιότητα;

Πολύ σύντομα αφότου ο Βέρνερ Χάιζενμπεργκ δημιούργησε τη νέα κβαντική φυσική, κάτι απροσδόκητο βγήκε από τα μαθηματικά του, η έκφραση:

Δ x Δ p ≳ h 4 π {\displaystyle \Delta x\,\Delta p\gtrsim {\frac {h}{4\pi }}\qquad \qquad \qquad \qquad }

Το εύρος του σφάλματος στη θέση (x) επί το εύρος του σφάλματος στην ορμή (p) είναι περίπου ίσο ή μεγαλύτερο από τη σταθερά του Planck διαιρούμενη διά 4π.

Τα σύμβολα αυτά μεταφράζουν σε μαθηματική μορφή αυτό που έχετε ήδη δει στις παραπάνω εικόνες. Τα σύμβολα λένε, με σαφή τρόπο, ότι δεν μπορείτε να είστε απόλυτα σίγουροι για το πού βρίσκεται κάτι και πού πηγαίνει. Αν ξεκαθαρίζετε περισσότερο για το πού βρίσκεται κάθε φορά, τότε έχετε λιγότερη ιδέα για το πού πηγαίνει και πόσο γρήγορα. Αν γίνετε πιο σαφής για το πού πηγαίνει και πόσο γρήγορα ανά πάσα στιγμή, τότε έχετε λιγότερη ιδέα για το πού βρίσκεται αυτή τη στιγμή.

Οι επιστήμονες είχαν ήδη μάθει γιατί ορισμένες ουσίες εκπέμπουν χαρακτηριστικά χρώματα φωτός όταν θερμαίνονται ή διεγείρονται με άλλο τρόπο. Ο Χάιζενμπεργκ προσπαθούσε να εξηγήσει γιατί αυτά τα χρώματα έχουν μια χαρακτηριστική φωτεινότητα. Δεν θα ήταν αρκετό αν αυτός και οι άλλοι επιστήμονες είχαν απλώς πει: "Ε, έτσι είναι". Ήταν σίγουροι ότι έπρεπε να υπάρχει ένας καλός λόγος για αυτές τις διαφορές και για το γεγονός ότι οι αναλογίες μεταξύ των δυνάμεων των φωτεινών γραμμών ήταν πάντα οι ίδιες για κάθε δείγμα ενός στοιχείου.

Δεν είχε ιδέα ότι επρόκειτο να πέσει πάνω σε ένα κρυμμένο μυστικό της φύσης όταν ξεκίνησε να ανακαλύψει την εξήγηση για την ένταση των χρωματιστών γραμμών που χαρακτηρίζουν κάθε στοιχείο. Η μελέτη της κβαντομηχανικής είχε ήδη δείξει γιατί το υδρογόνο έχει τέσσερις φωτεινές γραμμές στο τμήμα του φάσματος που μπορεί να δει ο άνθρωπος. Πρέπει να φάνηκε ότι το επόμενο πράγμα που έπρεπε να μάθει θα ήταν απλώς πώς να υπολογίσει τη φωτεινότητά τους. Το υδρογόνο φαινόταν να είναι το προφανές μέρος για να ξεκινήσει κανείς, δεδομένου ότι το υδρογόνο έχει μόνο ένα ηλεκτρόνιο να αντιμετωπίσει και μόνο τέσσερις γραμμές στο ορατό τμήμα του φάσματος. Σίγουρα θα πρέπει να υπάρχει κάποιος καλός λόγος για να μην είναι εξίσου φωτεινά. Η εξήγηση για τη φωτεινότητα των διαφορετικού χρώματος γραμμών του νέον και των άλλων στοιχείων μπορούσε να περιμένει.

 

Ο Χάιζενμπεργκ άρχισε να εργάζεται πάνω στην κβαντική φυσική προσαρμόζοντας τις κλασικές εξισώσεις για τον ηλεκτρισμό, οι οποίες είναι πολύ περίπλοκες εξ αρχής, οπότε τα μαθηματικά πίσω από την εργασία του 1925 ήταν πολύ δύσκολο να ακολουθηθούν.

Προσπαθούσε να βρει τον σωστό τρόπο υπολογισμού της έντασης των φωτεινών γραμμών στο φάσμα της λυχνίας υδρογόνου. Έπρεπε να βρει μια σχετική ποσότητα που ονομάζεται "πλάτος" και να πολλαπλασιάσει το πλάτος επί το πλάτος (ή με άλλα λόγια έπρεπε να τετραγωνίσει το πλάτος) για να πάρει την ένταση που ήθελε. Έπρεπε να βρει πώς να εκφράσει το πλάτος με τρόπο που να λαμβάνει υπόψη το γεγονός ότι οι λαμπτήρες υδρογόνου δεν ακτινοβολούν σε όλες τις συχνότητες και δεν ακτινοβολούν σε ένα συνεχές φάσμα συχνοτήτων στο τμήμα του φάσματος που μπορούν να δουν οι άνθρωποι. Ο Χάιζενμπεργκ βρήκε έναν αξιοσημείωτο νέο τρόπο υπολογισμού του πλάτους.

Η παράξενη εξίσωση|εξίσωση που ανακάλυψε ο Χάιζενμπεργκ και χρησιμοποίησε για να κάνει τον πολλαπλασιασμό μιας κβαντικής ποσότητας (π.χ. της θέσης) με μια άλλη (π.χ. της ορμής) δημοσιεύτηκε σε αυτό που έχει ονομαστεί "η "μαγική" εργασία του Χάιζενμπεργκ τον Ιούλιο του 1925".

C ( n , n - b ) = ∑ a A ( n , n - a ) B ( n - a , n - b ) {\displaystyle C(n,n-b)=\sum _{a}^{}\\,A(n,n-a)B(n-a,n-b)}

Τα παραπάνω μαθηματικά φαίνονται πολύ δύσκολα, αλλά τα μαθηματικά που οδηγούν σε αυτά είναι πολύ πιο δύσκολα και είναι εξαιρετικά δύσκολο να κατανοηθούν. Δίνονται εδώ απλώς για να δείξουν πώς φαίνονται. Η εργασία του Χάιζενμπεργκ είναι ένα ιστορικό ορόσημο. Πολλοί από τους φυσικούς που διάβασαν την εργασία του είπαν ότι δεν μπορούσαν να διαφωνήσουν με τα συμπεράσματά του, αλλά ότι δεν μπορούσαν να ακολουθήσουν την εξήγησή του για το πώς έφτασε σε αυτά τα συμπεράσματα. Οι αρχικές εξισώσεις που χρησιμοποίησε ο Χάιζενμπεργκ περιλάμβαναν σειρές Fourier και περιλάμβαναν πολλούς παράγοντες. Θα επανέλθουμε στην παραπάνω εξίσωση επειδή αποτελεί ένα είδος συνταγής για τη σύνταξη και τον πολλαπλασιασμό πινάκων.

Οι νέες εξισώσεις έπρεπε να είναι τόσο παράξενες και ασυνήθιστες επειδή ο Χάιζενμπεργκ περιέγραφε έναν παράξενο κόσμο στον οποίο ορισμένα πράγματα, όπως οι τροχιές των ηλεκτρονίων, δεν γίνονται αργά μεγαλύτερες ή μικρότερες. Τα νέα είδη αλλαγών περιλαμβάνουν άλματα και μεγάλα κενά μεταξύ των αλμάτων. Τα ηλεκτρόνια μπορούν να κάνουν άλματα μόνο μεταξύ ορισμένων τροχιών, και η ενέργεια που κερδίζεται ή χάνεται κατά την αλλαγή μεταξύ των τροχιών παράγεται όταν απορροφάται ένα φωτόνιο της κατάλληλης ενέργειας ή παράγεται ένα νέο φωτόνιο της κατάλληλης ενέργειας. Εάν τα ηλεκτρόνια στα άτομα υδρογόνου μεταπηδούν (πέφτουν) συχνότερα μεταξύ δύο συγκεκριμένων τροχιών, τότε θα εκπέμπονται περισσότερα φωτόνια σε αυτό το ενεργειακό επίπεδο και έτσι το φως που παράγεται σε αυτό το επίπεδο θα είναι το πιο έντονο.

Ήταν δύσκολο να κάνουμε εξισώσεις που έχουν κατασκευαστεί για συνεχή φάσματα (αυτό που βλέπετε όταν περνάτε το φως του ήλιου μέσα από ένα πρίσμα) να ταιριάζουν σε φάσματα που έχουν μόνο μερικές μέγιστες συχνότητες μεταξύ των οποίων δεν υπάρχει τίποτα. Σχεδόν όλα όσα είχαν ήδη μάθει για το φως και την ενέργεια είχαν γίνει με μεγάλα αντικείμενα όπως αναμμένα κεριά ή ήλιοι, και όλα αυτά τα μεγάλα αντικείμενα παράγουν συνεχή φάσματα. Παρόλο που αυτά τα συνηθισμένου μεγέθους πράγματα ήταν εύκολο να γίνουν πειράματα με αυτά, είχε πάρει πολύ χρόνο για να καταλάβουμε τους νόμους (φυσικούς)νόμους που τα διέπουν. Τώρα οι φυσικοί είχαν να κάνουν με πράγματα πολύ μικρά για να τα δουν, πράγματα που δεν παρήγαγαν συνεχή φάσματα, και προσπαθούσαν να βρουν έναν τρόπο να πάρουν τουλάχιστον στοιχεία από αυτά που ήδη γνώριζαν, τα οποία θα τους βοηθούσαν να βρουν τους νόμους αυτών των μικρών και διακεκομμένων πηγών φωτός.

Οι αρχικές εξισώσεις αφορούσαν ένα είδος δονούμενου σώματος που θα παρήγαγε ένα κύμα, λίγο σαν τον τρόπο με τον οποίο ένα γλωσσίδι σε ένα όργανο θα παρήγαγε ένα ηχητικό κύμα μιας χαρακτηριστικής συχνότητας. Υπήρχε λοιπόν κίνηση προς τα πίσω και προς τα εμπρός (όπως η δόνηση ενός καλαμιού) και υπήρχε ένα εκπεμπόμενο κύμα που μπορούσε να γραφεί ως ημιτονοειδές κύμα. Πολλά από αυτά που είχαν προηγουμένως υπολογιστεί για τη φυσική σε ατομικό επίπεδο είχαν να κάνουν με τα ηλεκτρόνια που κινούνται γύρω από τους πυρήνες. Όταν μια μάζα κινείται σε τροχιά, όταν περιστρέφεται γύρω από κάποιο είδος κόμβου, έχει αυτό που ονομάζεται "στροφορμή". Η στροφορμή είναι ο τρόπος με τον οποίο κάτι όπως ένα καρουζέλ θα συνεχίσει να περιστρέφεται αφού οι άνθρωποι σταματήσουν να το σπρώχνουν. Τα μαθηματικά που χρησιμοποιούνται για τον υπολογισμό της φάσης και της στροφορμής είναι πολύπλοκα. Συν τοις άλλοις, ο Χάιζενμπεργκ δεν έδειξε όλους τους υπολογισμούς του στην εργασία του 1925, οπότε ακόμη και οι καλοί μαθηματικοί μπορεί να δυσκολευτούν να συμπληρώσουν όσα δεν είπε.

Παρόλο που πολλοί φυσικοί είπαν ότι δεν μπορούσαν να καταλάβουν τα διάφορα μαθηματικά βήματα στην επαναστατική εργασία του Χάιζενμπεργκ, ένα πρόσφατο άρθρο που προσπαθεί να εξηγήσει πώς ο Χάιζενμπεργκ πήρε το αποτέλεσμά του χρησιμοποιεί είκοσι σελίδες γεμάτες μαθηματικά. Ακόμη και αυτό το άρθρο δεν είναι εύκολο να κατανοηθεί. Τα μαθηματικά ξεκίνησαν με κάποια πραγματικά δύσκολα πράγματα και τελικά θα παρήγαγαν κάτι σχετικά απλό που φαίνεται στην κορυφή αυτού του άρθρου. Το να φτάσουμε στο απλούστερο αποτέλεσμα δεν ήταν εύκολο, και δεν πρόκειται να προσπαθήσουμε να δείξουμε τη διαδικασία για να φτάσουμε από μια ξεπερασμένη εικόνα του σύμπαντος στη νέα κβαντική φυσική. Χρειαζόμαστε μόνο αρκετές λεπτομέρειες για να δείξουμε ότι σχεδόν αμέσως μόλις ο Χάιζενμπεργκ έκανε την ανακάλυψή του ήρθε στο προσκήνιο ένα μέρος του τρόπου λειτουργίας του σύμπαντος που κανείς δεν είχε δει ποτέ πριν.

Ο Χάιζενμπεργκ πρέπει να ήταν πολύ ενθουσιασμένος αλλά και πολύ κουρασμένος όταν, αργά το βράδυ, έκανε τελικά την ανακάλυψή του και άρχισε να αποδεικνύει στον εαυτό του ότι θα λειτουργούσε. Σχεδόν αμέσως παρατήρησε κάτι περίεργο, κάτι που νόμιζε ότι ήταν ένα ενοχλητικό μικρό πρόβλημα που θα μπορούσε να εξαφανίσει με κάποιο τρόπο. Αποδείχθηκε όμως ότι αυτή η μικρή ενόχληση ήταν μια μεγάλη ανακάλυψη.

Ο Χάιζενμπεργκ εργαζόταν προς την κατεύθυνση του πολλαπλασιασμού των πλατών με τα πλάτη, και τώρα ο Χάιζενμπεργκ είχε έναν καλό τρόπο να εκφράσει το πλάτος χρησιμοποιώντας τη νέα του εξίσωση. Φυσικά σκεφτόταν τον πολλαπλασιασμό και το πώς θα πολλαπλασίαζε πράγματα που δίνονταν με όρους περίπλοκων εξισώσεων.

Ο Χάιζενμπεργκ συνειδητοποίησε ότι εκτός από τον τετραγωνισμό του πλάτους θα ήθελε τελικά να πολλαπλασιάσει τη θέση με την ορμή, ή να πολλαπλασιάσει την ενέργεια με το χρόνο, και φαινόταν ότι θα είχε διαφορά αν γύριζε τη σειρά σε αυτές τις νέες περιπτώσεις. Ο Χάιζενμπεργκ δεν πίστευε ότι θα έπρεπε να έχει σημασία αν πολλαπλασιάζει κανείς τη θέση με την ορμή ή αν πολλαπλασιάζει την ορμή με τη θέση. Αν ήταν απλοί αριθμοί, δεν θα υπήρχε κανένα πρόβλημα. Αλλά ήταν και οι δύο πολύπλοκες εξισώσεις, και το πώς έβρισκες τους αριθμούς για να τους βάλεις στις εξισώσεις αποδείχτηκε ότι ήταν διαφορετικό ανάλογα με τον τρόπο με τον οποίο ξεκινούσες. Στη φύση έπρεπε να μετρήσετε τη θέση και μετά να μετρήσετε την ορμή, ή αλλιώς έπρεπε να μετρήσετε την ορμή και μετά τη θέση, και στα μαθηματικά επικρατούσε η ίδια γενική κατάσταση. (Δείτε το αγγλικό λήμμα της Wikipedia Heisenberg's entryway to matrix mechanics αν θέλετε να μάθετε τις περίεργες λεπτομέρειες!) Οι μικροσκοπικές αλλά ενοχλητικές διαφορές μεταξύ των αποτελεσμάτων επρόκειτο να παραμείνουν, όσο κι αν ο Χάιζενμπεργκ ευχόταν να εξαφανιστούν.

Εκείνη την εποχή ο Χάιζενμπεργκ δεν μπορούσε να απαλλαγεί από αυτό το μικρό πρόβλημα, αλλά ήταν εξαντλημένος, οπότε παρέδωσε τη δουλειά του στον άμεσο προϊστάμενό του, τον Μαξ Μπορν, και πήγε διακοπές.

Ο Μαξ Μπορν ήταν ένας αξιόλογος μαθηματικός που σύντομα είδε ότι η εξίσωση που του είχε δώσει ο Χάιζενμπεργκ ήταν ένα είδος συνταγής για τη συγγραφή ενός πίνακα. Ο δρ Μπορν ήταν ένας από τους λίγους ανθρώπους εκείνη την εποχή που ενδιαφερόταν για αυτό το περίεργο είδος μαθηματικών που οι περισσότεροι άνθρωποι θεωρούσαν ότι δεν ήταν καλό για πολλά πράγματα. Ήξερε ότι οι πίνακες μπορούσαν να πολλαπλασιαστούν, οπότε το να κάνει κανείς όλους τους υπολογισμούς για τη λογιστική αντιμετώπιση ενός προβλήματος φυσικής μπορούσε να αντιμετωπιστεί πολλαπλασιάζοντας έναν πίνακα με έναν άλλο. Απλώς το να μπορεί να θέσει μια περίπλοκη διαδικασία σε μια τυποποιημένη και αποδεκτή μορφή θα την έκανε πιο εύκολη στην εργασία. Θα μπορούσε επίσης να διευκολύνει την αποδοχή της από άλλους ανθρώπους.

Ο Born ήταν τόσο καλός μαθηματικός που σχεδόν αμέσως συνειδητοποίησε ότι η αλλαγή της σειράς πολλαπλασιασμού των δύο πινάκων θα παρήγαγε διαφορετικό αποτέλεσμα, και τα αποτελέσματα θα διέφεραν κατά ένα μικρό ποσό. Το ποσό αυτό θα ήταν h/2πi. Στην καθημερινή ζωή, αυτή η διαφορά θα ήταν τόσο μικρή που δεν θα μπορούσαμε καν να τη δούμε.

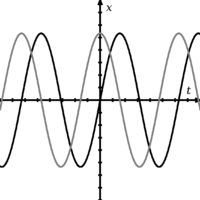
Δύο κύματα που είναι εκτός φάσης μεταξύ τους


Όταν ορισμένα μόρια διεγείρονται, εκπέμπουν ένα χαρακτηριστικό χρώμα.


Φάσμα υδρογόνου


Φάσμα νέον


Πλήρες οπτικό φάσμα του ήλιου. Δεν υπάρχουν κενά. Αυτό το διάγραμμα δείχνει τις εντάσεις στις διάφορες συχνότητες.

Σε μια τυπική θεωρία της αβεβαιότητας

Χρειάστηκαν μερικά χρόνια, αλλά ο Χάιζενμπεργκ κατάφερε να αποδείξει την Αρχή της Αβεβαιότητας, η οποία λέει ότι Δx × Δp = h/2, ο οποίος είναι ο αριθμός που προκύπτει από τις αρχικές εξισώσεις, αλλά αφήνει έξω το π και το i που έχουν να κάνουν με τις αλλαγές φάσης. Ο Χάιζενμπεργκ εξήγησε ότι αντλούσε την αρχή της αβεβαιότητας από αυτό το προηγούμενο αποτέλεσμα όταν έγραψε μια εργασία το 1927 παρουσιάζοντας αυτή τη θεωρία.

Η σταθερά που γράφεται h και ονομάζεται σταθερά του Planck, είναι ένας μυστηριώδης αριθμός που εμφανίζεται συχνά, γι' αυτό πρέπει να καταλάβουμε τι είναι αυτός ο μικρός αριθμός. Αριθμητικά, συνήθως δίνεται ως 6,62607×10^-34 J s (δευτερόλεπτα τζουλέ). Πρόκειται λοιπόν για ένα μέγεθος που περιλαμβάνει ενέργεια και χρόνο.

Ανακαλύφθηκε όταν ο Πλανκ συνειδητοποίησε ότι η ενέργεια ενός τέλειου ακτινοβολητή (που ονομάζεται ακτινοβολητής μαύρου σώματος) εκπέμπεται σε μονάδες συγκεκριμένου μεγέθους που ονομάζονται "κβάντα" (ο ενικός αριθμός αυτής της λέξης είναι "κβάντο"). Η ακτινοβολούμενη ενέργεια εκπέμπεται ως φωτόνια και η συχνότητα ενός φωτονίου είναι ανάλογη της "γροθιάς" που δίνει. Αντιλαμβανόμαστε τις διαφορετικές συχνότητες του ορατού φωτός ως διαφορετικά χρώματα. Στο ιώδες άκρο του φάσματος, κάθε φωτόνιο έχει σχετικά μεγάλη ποσότητα ενέργειας- στο κόκκινο άκρο του φάσματος κάθε φωτόνιο έχει σχετικά μικρή ποσότητα ενέργειας. Ο τρόπος υπολογισμού της ποσότητας ενέργειας ενός φωτονίου δίνεται από την εξίσωση E = hν (η ενέργεια ισούται με τη σταθερά του Planck επί το "nu" ή τη συχνότητα).

Η αρχή της αβεβαιότητας του Χάιζενμπεργκ Δx × Δp ≥ h μας λέει ότι κάθε φορά που προσπαθούμε να προσδιορίσουμε ορισμένα ζεύγη αριθμών μπορούμε να πλησιάσουμε τόσο κοντά και ότι αν προσπαθήσουμε να γίνουμε πιο σαφείς σε ένα από αυτά, δηλαδή αν προσπαθήσουμε να κάνουμε το Δx μικρότερο ώστε να έχουμε μια καλύτερη ιδέα για τη θέση κάποιου πράγματος, τότε θα πρέπει να μας δοθεί πίσω ένας μεγαλύτερος αριθμός για τον άλλο αριθμό του ζεύγους και ότι το ποσό κατά το οποίο απέχουν τα δύο είναι στενά συνδεδεμένο με το h.

Ένα άλλο ζεύγος φυσικών μεγεθών κινείται σύμφωνα με τη σχέση αβεβαιότητας: ΔΕ × Δt ≥ h, και αυτό το ζεύγος δείχνει, μεταξύ άλλων, ότι αν κοιτάξουμε στο διαστρικό διάστημα, σε κάποιο μέρος όπου δεν θα περιμέναμε να βρούμε τίποτα απολύτως, και μειώσουμε το Δt όλο και πιο κοντά στο 0, τότε για να διατηρηθεί η ισορροπία που φαίνεται στην εξίσωση το ΔΕ πρέπει να γίνεται όλο και μεγαλύτερο - και ξαφνικά κάτι με ορμή μπορεί να εμφανιστεί μόνο για αυτό το σύντομο χρονικό διάστημα.

Πώς εξηγείται αυτή η απροσδιοριστία (έλλειψη βεβαιότητας); Τι συμβαίνει στο Σύμπαν; Συχνά λέγεται ότι μια νέα θεωρία που είναι επιτυχής μπορεί να παρέχει νέες πληροφορίες για τα υπό διερεύνηση φαινόμενα. Ο Χάιζενμπεργκ δημιούργησε ένα μαθηματικό μοντέλο που προέβλεψε τις σωστές εντάσεις για το φάσμα των φωτεινών γραμμών του υδρογόνου, αλλά χωρίς να το επιδιώκει, ανακάλυψε ότι ορισμένα ζεύγη φυσικών μεγεθών αποκαλύπτουν μια απροσδόκητη αβεβαιότητα. Μέχρι εκείνη τη στιγμή κανείς δεν είχε ιδέα ότι οι μετρήσεις δεν μπορούσαν να γίνονται για πάντα όλο και πιο ακριβείς και ακριβείς. Το γεγονός ότι δεν μπορούσαν να γίνουν πιο σίγουρες, πιο οριστικές, ήταν μια εκπληκτική νέα ανακάλυψη. Πολλοί άνθρωποι δεν ήταν πρόθυμοι να το αποδεχτούν.

Ο Bohr και οι συνάδελφοί του υποστήριξαν ότι τα φωτόνια, τα ηλεκτρόνια κ.λπ. δεν έχουν ούτε θέση ούτε ορμή μέχρι να μετρηθούν. Αυτή η θεωρητική θέση προέκυψε από την ανακάλυψη της αβεβαιότητας και δεν ήταν απλώς κάποια προσωπική προτίμηση για το τι πρέπει να πιστεύουμε. Ο Bohr είπε ότι δεν γνωρίζουμε τίποτα για κάτι όπως ένα φωτόνιο ή ένα ηλεκτρόνιο μέχρι να το παρατηρήσουμε. Για να παρατηρήσουμε ένα τόσο μικρό πράγμα πρέπει να αλληλεπιδράσουμε με κάποιον τρόπο μαζί του. Στην καθημερινή ζωή είναι δυνατόν να κάνουμε κάτι σαν να περπατάμε δίπλα σε ένα αυτοκίνητο και ταυτόχρονα να σημειώνουμε τις φορές που αυτό περνάει από σημεία ενός πλέγματος που έχει σχεδιαστεί στο πεζοδρόμιο. Ίσως το βάρος του ίδιου του αυτοκινήτου να πιέζει μικρούς μοχλούς στο πεζοδρόμιο που θα απενεργοποιούν ρολόγια προσαρτημένα σε καθένα από αυτά και θα καταγράφουν το βάρος του αυτοκινήτου. Στο τέλος θα έχουμε μια σαφή καταγραφή του πού βρισκόταν το αυτοκίνητο σε διάφορες χρονικές στιγμές, και επίσης θα μπορούμε να υπολογίσουμε την κατεύθυνση της πορείας του και το βάρος του. Θα μπορούσαμε τότε να γνωρίζουμε, σε κάθε χρονική στιγμή του ρολογιού, τόσο τη θέση του όσο και την ορμή του (την ταχύτητά του πολλαπλασιασμένη επί τη μάζα του). Δεν θα μπορούσαμε καν να φανταστούμε ότι η δύναμη που απαιτείται για την κίνηση των μικρών μοχλών θα είχε οποιαδήποτε επίδραση στην πρόοδο του αυτοκινήτου. Δεν θα μπορούσαμε επίσης να φανταστούμε ότι το αυτοκίνητο δεν είχε καμία θέση ή τροχιά μεταξύ των σημείων του οδοστρώματος όπου υπάρχουν μοχλοί, ή ότι το αυτοκίνητο υπάρχει σε ένα είδος τρισδιάστατης θολούρας κατά τη διάρκεια αυτών των χρόνων και κατασταλάζει μόνο όταν πατάει έναν μοχλό. Ο κόσμος με τον οποίο είμαστε εξοικειωμένοι δεν αποκαλύπτει αυτά τα παράξενα είδη αλληλεπιδράσεων.

Για να εντοπίσουμε ένα πλοίο στη θάλασσα κατά τη διάρκεια της πιο σκοτεινής νύχτας θα μπορούσαμε να χρησιμοποιήσουμε έναν προβολέα, και αυτό το φως δεν θα διαταράξει τη θέση ή την κατεύθυνση του ταξιδιού του πλοίου, αλλά για να εντοπίσουμε ένα ηλεκτρόνιο με φως θα έπρεπε να το χτυπήσουμε με ένα ή περισσότερα φωτόνια που το καθένα έχει αρκετή ορμή για να διαταράξει τη θέση και την τροχιά του ηλεκτρονίου. Ο εντοπισμός του ηλεκτρονίου με άλλα μέσα θα απαιτούσε την κράτησή του σε κάποιο είδος φυσικού περιορισμού που θα τερμάτιζε επίσης την προς τα εμπρός κίνησή του.

Για τον εντοπισμό ενός φωτονίου, το καλύτερο που μπορεί να γίνει χωρίς να τερματιστεί η κίνησή του προς τα εμπρός είναι να περάσει μέσα από μια κυκλική τρύπα σε ένα φράγμα. Αν γνωρίζουμε τη χρονική στιγμή κατά την οποία εκπέμφθηκε το φωτόνιο (από ένα λέιζερ, για παράδειγμα) και τη χρονική στιγμή που το φωτόνιο φτάνει σε μια οθόνη ανίχνευσης, όπως μια ψηφιακή φωτογραφική μηχανή, τότε είναι δυνατόν να υπολογίσουμε το χρόνο που απαιτείται για να διανύσει αυτή την απόσταση και τη χρονική στιγμή κατά την οποία το φωτόνιο περνούσε μέσα από την οπή. Ωστόσο, για να μπορέσει το φωτόνιο να περάσει από αυτήν, η κυκλική οπή πρέπει να έχει διάμετρο μεγαλύτερη από το μέγεθος του φωτονίου. Όσο μικρότερη γίνεται η κυκλική οπή, τόσο πιο κοντά ερχόμαστε στο να γνωρίζουμε την ακριβή θέση του φωτονίου καθώς περνάει μέσα από αυτήν. Ωστόσο, δεν μπορούμε ποτέ να γνωρίζουμε αν το φωτόνιο είναι εκτός κέντρου εκείνη τη στιγμή. Αν η τρύπα έχει ακριβώς το ίδιο μέγεθος με το φωτόνιο, αυτό δεν θα περάσει. Καθώς η διάμετρος της οπής μειώνεται, η ορμή ή η κατεύθυνση του φωτονίου καθώς φεύγει από την οπή αλλάζει όλο και πιο πολύ.

Ο Νιλς Μπορ και οι συνάδελφοί του υποστήριξαν ότι έχουμε μεγάλο πρόβλημα αν υποθέσουμε ότι ισχύει για τα πράγματα που είναι πολύ μικρά για να τα δούμε ακόμη και με μικροσκόπιο οτιδήποτε για το οποίο έχουμε αποδείξεις μόνο στην κλίμακα της καθημερινής ζωής. Στην καθημερινή ζωή, τα πράγματα έχουν μια συγκεκριμένη θέση ανά πάσα στιγμή. Στην ατομική κλίμακα, δεν έχουμε καμία απόδειξη για να υποστηρίξουμε αυτό το συμπέρασμα. Στην καθημερινή ζωή, τα πράγματα έχουν μια συγκεκριμένη χρονική στιγμή κατά την οποία συμβαίνουν. Στην ατομική κλίμακα, δεν έχουμε στοιχεία που να υποστηρίζουν αυτό το συμπέρασμα. Στην καθημερινή ζωή, αν κάποιος παρατηρεί ένα εργοστάσιο από τη νυχτερινή βάρδια της πρώτης ημέρας μέχρι την πρωινή βάρδια της δεύτερης ημέρας και βλέπει ένα έτοιμο αυτοκίνητο να βγαίνει στην αποβάθρα, δεν θα είχε νόημα να πει ότι είναι αδύνατο να πει κανείς αν παραδόθηκε κατά τη διάρκεια της νυχτερινής ή της πρωινής βάρδιας. Αλλά στην ατομική κλίμακα, μπορούμε να δείξουμε περιπτώσεις όπου πρέπει να μετρήσουμε ένα και μόνο φωτόνιο σαν να έχει παραχθεί σε δύο χρονικές στιγμές. (Αν αυτό δεν είναι αρκετά κακό, μπορούμε επίσης να δείξουμε περιπτώσεις όπου ένα μόνο φωτόνιο παράγεται από δύο γειτονικά λέιζερ).

Μέρος της δυσκολίας να ανακαλύψουμε τι συμβαίνει στην ατομική κλίμακα είναι ότι θα θέλαμε να γνωρίζουμε τόσο πού βρίσκεται κάτι όσο και ποια είναι η τροχιά του, και να γνωρίζουμε και τα δύο πράγματα για την ίδια στιγμή, αλλά δεν μπορούμε να μετρήσουμε ταυτόχρονα τη θέση και την τροχιά. Είτε μετράμε την ορμή ενός φωτονίου ή ενός ηλεκτρονίου σε μια στιγμή και στη συνέχεια, χωρίς μεγαλύτερη καθυστέρηση από την απαραίτητη, μετράμε τη θέση του, είτε αλλάζουμε τα πράγματα και μετράμε πρώτα τη θέση και μετά την ορμή. Το πρόβλημα είναι ότι κάνοντας την πρώτη να πάρει μια αρκετά συγκεκριμένη μορφή (πιέζοντας την με κάποιο τρόπο) αυξάνουμε την αβεβαιότητα που εμπεριέχεται στην επόμενη μέτρηση. Αν οι αρχικές μας μετρήσεις ήταν τόσο ακατέργαστες ώστε να εισάγονται πολλά σφάλματα σε κάθε μία από αυτές, τότε θα μπορούσαμε να βελτιώσουμε τα πράγματα χρησιμοποιώντας ένα ελαφρύτερο άγγιγμα για να κάνουμε κάθε μία από αυτές, αλλά δεν θα μπορούσαμε ποτέ να ξεπεράσουμε ένα ορισμένο όριο ακρίβειας.

Γνωρίζουμε από την καθημερινή ζωή ότι η προσπάθεια να ζυγίσουμε κάτι σε μια ζυγαριά μπάνιου που είναι τοποθετημένη πάνω σε ένα πλυντήριο ρούχων σε κύκλο στυψίματος θα δώσει ανακριβή αποτελέσματα, επειδή η βελόνα της ζυγαριάς θα κουνιέται άσχημα. Μπορούμε να απενεργοποιήσουμε το πλυντήριο ρούχων. Αλλά για πολύ ακριβείς μετρήσεις διαπιστώνουμε ότι τα φορτηγά που περνούν από τη γειτονιά κάνουν τη βελόνα να κουνιέται, οπότε μπορούμε να τοποθετήσουμε τη ζυγαριά πάνω σε κάτι για να την απομονώσουμε από τις εξωτερικές διαταραχές. Πιστεύουμε ότι μπορούμε να εξαλείψουμε τις δονήσεις αρκετά ώστε να έχουμε αποτελέσματα τόσο ακριβή όσο θέλουμε. Ποτέ δεν λαμβάνουμε υπόψη ότι το ίδιο το πράγμα πάνω στη ζυγαριά δονείται ή ότι διαθέτει μια απροσδιόριστη ορμή.

Επιχειρηματολογώντας προς τα πίσω από την Αρχή της Αβεβαιότητας, φαίνεται ότι στην πραγματικότητα δεν υπάρχει οριστική θέση και οριστική ορμή για οποιοδήποτε πράγμα ατομικής κλίμακας, και ότι οι πειραματιστές μπορούν μόνο να επιβάλλουν την οριστικότητα των πραγμάτων εντός του ορίου που καθορίζεται από την Αρχή της Αβεβαιότητας. Ο Bohr και οι συνάδελφοί του υποστήριξαν μόνο ότι δεν μπορούμε να γνωρίζουμε τίποτα χωρίς να κάνουμε μετρήσεις, και όταν γίνονται μετρήσεις μπορούμε να ωθήσουμε τα πράγματα προς την κατεύθυνση μιας πιο συγκεκριμένης θέσης ή μιας πιο συγκεκριμένης ορμής, αλλά ότι δεν μπορούμε να έχουμε την απόλυτη οριστικότητα ή βεβαιότητα που θα θέλαμε. Άλλοι όμως έλαβαν σοβαρά υπόψη τους την πιθανότητα αυτή και υποστήριξαν ότι αν τα μαθηματικά είναι σωστά, τότε δεν μπορεί να υπάρξει οριστικότητα ή βεβαιότητα στον κόσμο του εξαιρετικά μικρού. Η φύση της επιστήμης είναι ότι τα μαθηματικά είναι μόνο ένα μοντέλο της πραγματικότητας, και δεν υπάρχει καμία εγγύηση ότι είναι ένα σωστό μοντέλο.

Τα μαθηματικά και οι πρακτικές συνέπειες των πραγμάτων που προβλέπουν τα μαθηματικά είναι τόσο αξιόπιστα που είναι πολύ δύσκολο να διαφωνήσεις μαζί τους, αλλά αυτό που λένε τα μαθηματικά για τον πραγματικό κόσμο έχει δημιουργήσει διάφορες διαφορετικές ιδέες. Μεταξύ των επιστημόνων που συνεργάστηκαν με τον Νιλς Μπορ στην Κοπεγχάγη, η αρχή της αβεβαιότητας θεωρήθηκε ότι σε ένα στοιχειώδες επίπεδο το φυσικό σύμπαν δεν υπάρχει με ντετερμινιστική μορφή. Αντίθετα, είναι μια συλλογή πιθανοτήτων ή δυνατοτήτων.

Σε αντίθεση με την ιστορία που υφαίνεται γύρω από τα μαθηματικά από την ομάδα της Κοπεγχάγης, υπάρχουν και άλλες ιστορίες, όπως η "ερμηνεία των πολλαπλών συμπάντων" που λέει ότι κάθε φορά που υπάρχουν πολλαπλά πιθανά αποτελέσματα σύμφωνα με την κβαντική θεωρία, κάθε αποτέλεσμα εμφανίζεται στο δικό του νέο σύμπαν. Ο Αϊνστάιν υποστήριξε ότι δεν υπάρχουν πολλαπλά πιθανά αποτελέσματα, άρα υπάρχει μόνο ένα σύμπαν και αυτό είναι καθορισμένο, ή, όπως το έθεσε, "ο Θεός δεν παίζει ζάρια".

Αν το h ήταν η μικρότερη δυνατή ποσότητα ενέργειας, τότε η βασική εξίσωση που δείχνει την ενέργεια που περιέχεται στα φωτόνια διαφόρων συχνοτήτων δεν θα ισορροπούσε. Θα ήταν λάθος.

Αντιρρήσεις κατά της αρχής της αβεβαιότητας

Ο Άλμπερτ Αϊνστάιν είδε ότι η νέα κβαντομηχανική υπονοούσε την έλλειψη θέσης και ορμής στο χρόνο πριν από τη διεξαγωγή των μετρήσεων και διαφώνησε έντονα. Πίστευε ακράδαντα ότι τα πράγματα είχαν συγκεκριμένες θέσεις και συγκεκριμένες ορμές πριν από τη μέτρησή τους και ότι το γεγονός ότι η μέτρηση του ενός από ένα ζεύγος πραγμάτων και η διατάραξη της δυνατότητας ακριβούς μέτρησης του άλλου δεν συνηγορεί υπέρ της έλλειψης ενός από τα δύο εκ των προτέρων. Αυτός και δύο συνάδελφοί του έγραψαν αυτό που έμεινε γνωστό ως "έγγραφο EPR". Αυτό το έγγραφο υποστηρίζει ότι πρέπει να υπάρχουν χαρακτηριστικά που να καθορίζουν τη θέση και την ορμή και ότι αν μπορούσαμε να τα δούμε ή αν μπορούσαμε να πάρουμε πληροφορίες γι' αυτά, τότε θα μπορούσαμε να γνωρίζουμε και να προβλέψουμε μαθηματικά τη θέση και την ορμή. Για μεγάλο χρονικό διάστημα οι άνθρωποι πίστευαν ότι δεν υπήρχε τρόπος να αποδειχθεί ή να διαψευστεί αυτό που για τον Αϊνστάιν ήταν ένα άρθρο πίστης. Το επιχείρημα ήταν πολύ παραγωγικό, διότι οδήγησε σε όλες τις σύγχρονες εξελίξεις στον τομέα της διεμπλοκής.

Μαθηματικά, ο Αϊνστάιν έχει αποδειχθεί λάθος. Το 1964 ο Τζον Στιούαρτ Μπελ ανέπτυξε μια μαθηματική μέθοδο για να διακρίνει μεταξύ της συμπεριφοράς δύο σωματιδίων που έχουν καθορισμένες καταστάσεις που είναι απλώς άγνωστες στα δύο άτομα που τα ερευνούν, και δύο σωματιδίων που έχουν περιπλεγμένες καταστάσεις που είναι απροσδιόριστες ή αβέβαιες μέχρι να μετρηθούν. Η μέθοδός του δείχνει ότι οι πιθανότητες για την εξαγωγή συγκεκριμένων αποτελεσμάτων είναι διαφορετικές υπό τις δύο διαφορετικές παραδοχές. Το έργο του ονομάζεται θεώρημα του Μπελ ή ανισότητα του Μπελ. Πειράματα έχουν δείξει ότι η φύση συμπεριφέρεται όπως την περιγράφει ο Μπελ.

Μια άλλη διαδρομή προς την αβεβαιότητα

Οι αρχικές συζητήσεις για την αρχή της αβεβαιότητας του Χάιζενμπεργκ βασίζονταν σε ένα μοντέλο που δεν θεωρούσε ότι τα σωματίδια της ύλης, όπως τα ηλεκτρόνια, τα πρωτόνια κ.λπ. έχουν μήκος κύματος. Το 1926 ο Louis de Broglie έδειξε ότι όλα τα πράγματα, όχι μόνο τα φωτόνια, έχουν τη δική τους συχνότητα. Τα πράγματα έχουν κυματική και σωματιδιακή φύση, όπως ακριβώς και τα φωτόνια. Αν προσπαθήσουμε να κάνουμε το κύμα ενός πράγματος όπως ένα πρωτόνιο πιο στενό και πιο ψηλό, αυτό θα έκανε τη θέση του πιο ξεκάθαρη, αλλά τότε η ορμή του θα γινόταν λιγότερο καλά καθορισμένη. Αν προσπαθήσουμε να κάνουμε το μέρος της ορμής μιας κυματικής περιγραφής πιο σαφές, δηλαδή να το κάνουμε να παραμείνει σε ένα στενότερο εύρος τιμών, τότε η κορυφή του κύματος θα εξαπλωθεί και η θέση του θα γίνει λιγότερο καθορισμένη.

Το κύμα που αποτελεί μέρος της περιγραφής ενός φωτονίου δεν είναι, σύμφωνα με την κβαντομηχανική, το ίδιο είδος πράγματος με ένα κύμα στην επιφάνεια του ωκεανού ή με τις περιοχές του συμπιεσμένου και του αραιωμένου αέρα που αποτελούν τα ηχητικά κύματα. Αντίθετα, αυτά τα κύματα έχουν κορυφές ή περιοχές υψηλού πλάτους που έχουν να κάνουν με την πιθανότητα να βρεθεί κάτι σε εκείνο το σημείο του χώρου και του χρόνου. Πιο συγκεκριμένα, είναι το τετράγωνο του πλάτους που δίνει την πιθανότητα εμφάνισης κάποιου φαινομένου.

Το κύμα που εφαρμόζεται σε ένα φωτόνιο μπορεί να είναι ένα καθαρό ημιτονοειδές κύμα. Στην περίπτωση αυτή, το τετράγωνο της τιμής κάθε κορυφής θα έδινε την πιθανότητα παρατήρησης του φωτονίου στο συγκεκριμένο σημείο. Δεδομένου ότι τα πλάτη των ημιτονοειδών κυμάτων είναι παντού τα ίδια, η πιθανότητα να βρεθεί το φωτόνιο σε κάθε ένα από αυτά θα ήταν η ίδια. Έτσι, πρακτικά μιλώντας, η γνώση του κύματος για ένα από αυτά τα φωτόνια δεν θα έδινε καμία ένδειξη για το πού να το αναζητήσουμε. Από την άλλη πλευρά, η ορμή ενός φωτονίου σχετίζεται μαθηματικά με το πλάτος του κύματός του. Δεδομένου ότι στην περίπτωση αυτή έχουμε ένα καθαρό ημιτονοειδές κύμα, το πλάτος κάθε κύκλου του κύματος είναι το ίδιο και επομένως υπάρχει μόνο μία τιμή ορμής που σχετίζεται με αυτό το κύμα. Δεν θα γνωρίζαμε πού θα χτυπούσε το φωτόνιο, αλλά θα γνωρίζαμε ακριβώς πόσο δυνατά θα χτυπούσε.

Σε δέσμες φωτός που εστιάζουν σε κάποιο σημείο μιας οθόνης ανίχνευσης, τα κύματα που σχετίζονται με τα φωτόνια δεν είναι καθαρά ημιτονοειδή κύματα. Αντιθέτως, πρόκειται για κύματα με υψηλό πλάτος σε ένα σημείο και πολύ χαμηλότερα πλάτη εκατέρωθεν αυτής της υψηλότερης κορυφής. Μαθηματικά είναι δυνατόν να αναλυθεί ένα τέτοιο κύμα σε έναν αριθμό διαφορετικών ημιτονοειδών κυμάτων με διαφορετικά μήκη κύματος. Είναι λίγο πιο εύκολο να απεικονίσουμε το αντίστροφο αυτής της διαδικασίας εξετάζοντας ένα αρχικό ημιτονοειδές κύμα μιας συχνότητας στο οποίο προστίθεται ένα δεύτερο ημιτονοειδές κύμα διαφορετικού μήκους κύματος, στη συνέχεια ένα τρίτο, στη συνέχεια ένα τέταρτο κ.ο.κ. Το αποτέλεσμα θα είναι ένα σύνθετο κύμα που θα εμφανίζει μία υψηλή κορυφή και θα περιέχει ένα μεγάλο αριθμό κυμάτων διαφορετικού μήκους κύματος και επομένως διαφορετικής ορμής. Στην περίπτωση αυτή, η πιθανότητα να εμφανιστεί το φωτόνιο σε ένα συγκεκριμένο σημείο είναι εξαιρετικά υψηλή, αλλά η ορμή που μεταφέρει μπορεί να αποδειχθεί ότι σχετίζεται με το μήκος κύματος οποιουδήποτε από τα συστατικά κύματα. Με άλλα λόγια, η τιμή p = ħ/λ δεν είναι πλέον μια ενιαία τιμή, επειδή πρέπει να ληφθούν υπόψη όλα τα μήκη των συναρμολογημένων "κυμάτων διαφορετικού μήκους κύματος".

Η προσομοίωση δείχνει πώς μπορεί να μοντελοποιηθεί μαθηματικά η όξυνση της θέσης ενός σωματιδίου: Τοποθετήστε πολλές διαφορετικές κυματομορφές πάνω στο αρχικό ημιτονοειδές κύμα. Το κέντρο θα σχηματίσει μια όλο και υψηλότερη κορυφή και οι υπόλοιπες κορυφές θα αυξηθούν σε αριθμό αλλά θα μειωθούν σε ύψος επειδή θα παρεμβάλλονται μεταξύ τους. Έτσι, στο τέλος υπάρχουν πολλά διαφορετικά κύματα στην υπέρθεση, το καθένα με διαφορετικό μήκος κύματος και (με p = ħ/λ) διαφορετική ορμή, αλλά μόνο μια πολύ υψηλή κορυφή, μια κορυφή που αυξάνεται όλο και πιο ψηλά και στενεύει και μας δίνει κάτι όλο και πιο κοντά σε μια καθορισμένη θέση.

Για να κάνουμε την ορμή όλο και πιο συγκεκριμένη, θα πρέπει να αφαιρούμε όλο και περισσότερα από τα επάλληλα ημιτονοειδή κύματα, μέχρι να μείνει μόνο ένα απλό ημιτονοειδές κύμα. Με τον τρόπο αυτό θα μειώναμε προοδευτικά το ύψος της κεντρικής κορυφής και θα αυξάναμε προοδευτικά τα ύψη των ανταγωνιστικών θέσεων όπου θα μπορούσε κανείς να βρει το σωματίδιο.

Έτσι, όταν ξεκινάμε με μια κυματική εικόνα των υποατομικών σωματιδίων, συνήθως θα έχουμε πάντα να κάνουμε με περιπτώσεις με σχετικά ψηλές κεντρικές κορυφές και σχετικά πολλά μήκη κύματος των συνιστωσών. Ποτέ δεν θα υπάρξει μια ακριβής θέση ή μια ακριβής ορμή που θα προβλεφθεί κάτω από αυτές τις συνθήκες. Αν το μαθηματικό μοντέλο είναι μια ακριβής αναπαράσταση του πραγματικού κόσμου, τότε κανένα φωτόνιο ή άλλο υποατομικό σωματίδιο δεν έχει ούτε ακριβή θέση ούτε συγκεκριμένη ορμή. Όταν μετράμε ένα τέτοιο σωματίδιο, μπορούμε να επιλέξουμε μια μέθοδο που συμπιέζει περαιτέρω την κορυφή και την κάνει στενότερη, ή μπορούμε να επιλέξουμε μια μέθοδο που χαμηλώνει την κορυφή και εξισώνει τα μήκη κύματος των συστατικών. Ανάλογα με το τι μετράμε και πώς το μετράμε, μπορούμε να κάνουμε τη θέση μας να βγει πιο συγκεκριμένη ή μπορούμε να κάνουμε το εύρος της ορμής μας πιο στενό. Μπορούμε να φροντίσουμε κατά το σχεδιασμό του πειράματος να αποφύγουμε διάφορους τρόπους να ταρακουνήσουμε τη συσκευή, αλλά δεν μπορούμε να απαλλαγούμε από το γεγονός ότι δεν υπήρχε τίποτα απολύτως οριστικό εξ αρχής.

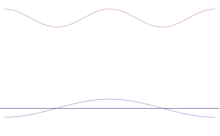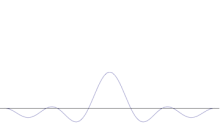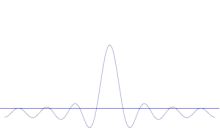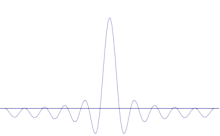
Η υπέρθεση πολλών επίπεδων κυμάτων. Το κυματοπακέτο γίνεται όλο και πιο εντοπισμένο με την προσθήκη πολλών κυμάτων. Ο μετασχηματισμός Fourier είναι μια μαθηματική πράξη που διαχωρίζει ένα κυματοπακέτο στα επιμέρους επίπεδα κύματά του. Σημειώστε ότι τα κύματα που παρουσιάζονται εδώ είναι πραγματικά μόνο για ενδεικτικούς σκοπούς, ενώ στην κβαντομηχανική η κυματοσυνάρτηση είναι γενικά μιγαδική.

Πολιτιστικές επιρροές

Η σημαντικότερη επιρροή της Αρχής της Αβεβαιότητας του Χάιζενμπεργκ ήταν στα επιχειρήματα σχετικά με την ελευθερία της βούλησης. Σύμφωνα με τις θεωρίες της κλασικής φυσικής είναι δυνατό να υποστηριχθεί ότι οι νόμοι της αιτίας και του αποτελέσματος είναι αμείλικτοι και ότι από τη στιγμή που το σύμπαν ξεκίνησε με έναν ορισμένο τρόπο, οι αλληλεπιδράσεις όλης της ύλης και της ενέργειας που θα συμβούν στο μέλλον θα μπορούσαν να υπολογιστούν από αυτή την αρχική κατάσταση. Εφόσον τα πάντα είναι απολύτως το αποτέλεσμα αυτού που προηγήθηκε, υποστήριζαν, κάθε απόφαση που λαμβάνει ένα ανθρώπινο ον και κάθε κατάσταση στην οποία μπαίνει αυτό το ανθρώπινο ον ήταν προκαθορισμένη από την αρχή του χρόνου. Επομένως, δεν έχουμε καμία επιλογή σε ό,τι κάνουμε.

Οι άνθρωποι που πιστεύουν στην ελευθερία της βούλησης υποστηρίζουν ότι οι νόμοι της κβαντομηχανικής δεν προβλέπουν τι θα συμβεί, αλλά μόνο τι είναι περισσότερο και τι λιγότερο πιθανό να συμβεί. Επομένως, κάθε πράξη είναι το αποτέλεσμα μιας σειράς τυχαίων "ρίψεων κέρματος" και καμία απόφαση δεν μπορεί να αναχθεί σε ένα σύνολο αναγκαίων προϋποθέσεων.

Οι εκφράσεις "κβαντικό άλμα" και "κβαντικό άλμα" έχουν γίνει συνηθισμένοι τρόποι να μιλάμε για τα πράγματα. Συνήθως οι άνθρωποι σκοπεύουν να περιγράψουν κάτι που περιλαμβάνει μια τεράστια αλλαγή που συμβαίνει σε σύντομο χρονικό διάστημα. Ο όρος στην πραγματικότητα αναφέρεται στον τρόπο με τον οποίο ένα ηλεκτρόνιο συμπεριφέρεται σε ένα άτομο είτε όταν απορροφά ένα φωτόνιο που έρχεται από το εξωτερικό και έτσι μεταπηδά από μια τροχιά γύρω από τον πυρήνα του ατόμου σε μια υψηλότερη τροχιά, είτε όταν εκπέμπει ένα φωτόνιο και έτσι πέφτει από μια υψηλότερη τροχιά σε μια χαμηλότερη τροχιά. Η ιδέα του Neils Bohr και των συναδέλφων του ήταν ότι το ηλεκτρόνιο δεν κινείται μεταξύ τροχιών, αλλά αντίθετα εξαφανίζεται από μια τροχιά και εμφανίζεται ακαριαία σε μια άλλη τροχιά. Έτσι, ένα κβαντικό άλμα δεν είναι στην πραγματικότητα κάποια κοσμοϊστορική αλλαγή, αλλά μια ξαφνική μικρή αλλαγή από έναν τομέα σε έναν άλλο.

Όταν οι άνθρωποι μετρούν κάποια διαδικασία σε υποατομική κλίμακα και η αρχή της αβεβαιότητας εκδηλώνεται, τότε μπορεί να ειπωθεί ότι η ανθρώπινη δράση έχει επηρεάσει το πράγμα που μετριέται. Η πραγματοποίηση μιας μέτρησης που αποσκοπεί στην απόκτηση μιας οριστικής ένδειξης της θέσης ενός σωματιδίου θα επηρεάσει αναπόφευκτα την ορμή του και ό,τι και αν γίνει για να μετρηθεί αυτή η ορμή το συντομότερο δυνατό μετά τη μέτρηση της θέσης του, οι πιθανότητες για το ποια ορμή θα ανακαλυφθεί δεν μπορεί παρά να έχουν μεταβληθεί. Έτσι, η αρχή της αβεβαιότητας μπορεί να εξηγήσει ορισμένα είδη παρεμβολών που παράγονται από ερευνητές και επηρεάζουν τα αποτελέσματα ενός πειράματος ή μιας παρατήρησης. Ωστόσο, δεν οφείλονται όλες οι επιδράσεις των παρατηρητών σε κβαντικά φαινόμενα ή στην αρχή της αβεβαιότητας. Τα υπόλοιπα είναι "φαινόμενα παρατηρητή" αλλά όχι κβαντικά φαινόμενα αβεβαιότητας.

Οι επιδράσεις των παρατηρητών περιλαμβάνουν όλα τα είδη των πραγμάτων που λειτουργούν στη συνηθισμένη ανθρώπινη κλίμακα των γεγονότων. Αν ένας ανθρωπολόγος προσπαθήσει να αποκτήσει μια σαφή εικόνα της ζωής σε μια πρωτόγονη κοινωνία, αλλά η παρουσία του αναστατώνει την κοινότητα που επισκέπτεται, τότε οι παρατηρήσεις που θα κάνει μπορεί να είναι πολύ παραπλανητικές. Ωστόσο, καμία από τις σχετικές αλληλεπιδράσεις δεν λαμβάνει χώρα στο επίπεδο που περιγράφεται από την κβαντομηχανική ή την αρχή της αβεβαιότητας.

Μερικές φορές η λέξη "κβαντική" χρησιμοποιείται για διαφημιστικούς σκοπούς για να υποδηλώσει κάτι νέο και ισχυρό. Για παράδειγμα, ο κατασκευαστής μικρών βενζινοκινητήρων, η Briggs and Stratton, διαθέτει μια σειρά τετρακύλινδρων κινητήρων χαμηλής ιπποδύναμης για βενζινοκίνητα χλοοκοπτικά μηχανήματα και παρόμοια εργαλεία κήπου που ονομάζει "Quantum".

Περισσότερες πληροφορίες

• Εισαγωγή στην κβαντική θεωρία, σ. 115 και σ. 158

J.P. McEvoy και Oscar Zarate