Σταθερά του Πλανκ

Ιστορικό

Σύμβολα που χρησιμοποιούνται σε αυτό το άρθρο.
Σύμβολο Σημασία E Ενέργεια h Σταθερά Planck k Σταθερά Boltzmann c ταχύτητα του φωτός λ μήκος κύματος ακτινοβολίας ν συχνότητα ακτινοβολίας T απόλυτη θερμοκρασία

Μεταξύ του 1670 και του 1900 οι επιστήμονες συζήτησαν τη φύση του φωτός. Ορισμένοι επιστήμονες πίστευαν ότι το φως αποτελείται από πολλά εκατομμύρια μικροσκοπικά σωματίδια. Άλλοι επιστήμονες πίστευαν ότι το φως ήταν κύμα.

Φως: κύματα ή σωματίδια;

Το 1678, ο Christiaan Huygens έγραψε το βιβλίο Traité de la lumiere ("Πραγματεία για το φως"). Πίστευε ότι το φως αποτελείται από κύματα. Είπε ότι το φως δεν μπορεί να αποτελείται από σωματίδια, επειδή το φως από δύο δέσμες δεν ανακλάται η μία από την άλλη. Το 1672, ο Ισαάκ Νεύτων έγραψε το βιβλίο Opticks. Πίστευε ότι το φως αποτελείται από κόκκινα, κίτρινα και μπλε σωματίδια τα οποία ονόμασε σωμάτια. Ο Νεύτωνας το εξήγησε αυτό με το "πείραμα των δύο πρισμάτων". Το πρώτο πρίσμα διέσπαγε το φως σε διαφορετικά χρώματα. Το δεύτερο πρίσμα συγχώνευσε αυτά τα χρώματα πίσω σε λευκό φως.

Κατά τη διάρκεια του 18ου αιώνα, η θεωρία του Νεύτωνα έτυχε της μεγαλύτερης προσοχής. Το 1803, ο Thomas Young περιέγραψε το "πείραμα διπλής σχισμής". Σε αυτό το πείραμα, το φως που περνά μέσα από δύο στενές σχισμές παρεμβάλλεται με τον εαυτό του. Αυτό προκαλεί ένα μοτίβο που δείχνει ότι το φως αποτελείται από κύματα. Για το υπόλοιπο του δέκατου ένατου αιώνα, η κυματική θεωρία του φωτός έτυχε της μεγαλύτερης προσοχής. Στη δεκαετία του 1860, ο Τζέιμς Κλερκ Μάξγουελ ανέπτυξε εξισώσεις που περιέγραφαν την ηλεκτρομαγνητική ακτινοβολία ως κύματα.

Η θεωρία της ηλεκτρομαγνητικής ακτινοβολίας αντιμετωπίζει το φως, τα ραδιοκύματα, τα μικροκύματα και πολλούς άλλους τύπους κυμάτων ως το ίδιο πράγμα, με τη διαφορά ότι έχουν διαφορετικά μήκη κύματος. Το μήκος κύματος του φωτός που μπορούμε να δούμε με τα μάτια μας είναι περίπου μεταξύ 400 και 600 nm. Το μήκος κύματος των ραδιοκυμάτων κυμαίνεται από 10 m έως 1500 m και το μήκος κύματος των μικροκυμάτων είναι περίπου 2 cm. Στο κενό, όλα τα ηλεκτρομαγνητικά κύματα ταξιδεύουν με την ταχύτητα του φωτός. Η συχνότητα του ηλεκτρομαγνητικού κύματος δίνεται από τη σχέση:

ν = c λ {\displaystyle \nu ={\frac {c}{\lambda }}}.

Τα σύμβολα ορίζονται εδώ.

Μαύρα ψυγεία σώματος

Όλα τα ζεστά πράγματα εκπέμπουν θερμική ακτινοβολία, η οποία είναι ηλεκτρομαγνητική ακτινοβολία. Για τα περισσότερα πράγματα στη Γη αυτή η ακτινοβολία είναι στην υπέρυθρη περιοχή, αλλά κάτι πολύ θερμό (1000 °C ή περισσότερο), εκπέμπει ορατή ακτινοβολία, δηλαδή φως. Στα τέλη της δεκαετίας του 1800 πολλοί επιστήμονες μελέτησαν τα μήκη κύματος της ηλεκτρομαγνητικής ακτινοβολίας από ακτινοβολητές μαύρων σωμάτων σε διαφορετικές θερμοκρασίες.

Νόμος Rayleigh-Jeans

Ο λόρδος Rayleigh δημοσίευσε για πρώτη φορά τα βασικά στοιχεία του νόμου Rayleigh-Jeans το 1900. Η θεωρία βασιζόταν στην κινητική θεωρία των αερίων. Ο Sir James Jeans δημοσίευσε μια πιο ολοκληρωμένη θεωρία το 1905. Ο νόμος συσχετίζει την ποσότητα και το μήκος κύματος της ηλεκτρομαγνητικής ενέργειας που εκπέμπεται από ένα ακτινοβολητή μαύρου σώματος σε διαφορετικές θερμοκρασίες. Η εξίσωση που το περιγράφει είναι η εξής:

B λ ( T ) = 2 c k T λ 4 {\displaystyle B_{\lambda }(T)={\frac {2ckT}{\lambda ^{4}}}}.

Για ακτινοβολία μεγάλου μήκους κύματος, τα αποτελέσματα που προβλέπονταν από την εξίσωση αυτή αντιστοιχούσαν καλά με τα πρακτικά αποτελέσματα που προέκυψαν σε εργαστήριο. Ωστόσο, για τα μικρά μήκη κύματος (υπεριώδες φως) η διαφορά μεταξύ θεωρίας και πρακτικής ήταν τόσο μεγάλη που απέκτησε το παρατσούκλι "η υπεριώδης καταστροφή".

Νόμος του Planck

το 1895 ο Wien δημοσίευσε τα αποτελέσματα των μελετών του σχετικά με την ακτινοβολία από ένα μαύρο σώμα. Ο τύπος του ήταν:

B λ ( T ) = 2 h c 2 λ 5 e - h c λ k T {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}e^{-{\frac {hc}{\lambda kT}}}} .

Αυτός ο τύπος λειτούργησε καλά για ηλεκτρομαγνητική ακτινοβολία μικρού μήκους κύματος, αλλά δεν λειτούργησε καλά με μεγάλα μήκη κύματος.

Το 1900 ο Μαξ Πλανκ δημοσίευσε τα αποτελέσματα των μελετών του. Προσπάθησε να αναπτύξει μια έκφραση για την ακτινοβολία μαύρου σώματος εκφρασμένη ως προς το μήκος κύματος, υποθέτοντας ότι η ακτινοβολία αποτελείται από μικρά κβάντα και στη συνέχεια να δει τι συμβαίνει αν τα κβάντα γίνουν απείρως μικρά. (Πρόκειται για μια τυπική μαθηματική προσέγγιση). Η έκφραση ήταν:

B λ ( T ) = 2 h c 2 λ 5 1 e h c λ k T - 1 {\displaystyle B_{\lambda }(T)={\frac {2hc^{2}}{\lambda ^{5}}}~{\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}}} .

Αν το μήκος κύματος του φωτός επιτραπεί να γίνει πολύ μεγάλο, τότε μπορεί να αποδειχθεί ότι οι σχέσεις Raleigh-Jeans και Planck είναι σχεδόν ταυτόσημες.

Υπολόγισε τα h και k και διαπίστωσε ότι

h = 6,55×10 ⁻²⁷erg-sec.

k = 1,34×10⁻¹⁶erg-deg ^-1.

Οι τιμές είναι κοντά στις σύγχρονες αποδεκτές τιμές 6,62606×10⁻³⁴ και 1,38065×10⁻¹⁶ αντίστοιχα. Ο νόμος του Πλανκ συμφωνεί καλά με τα πειραματικά δεδομένα, αλλά η πλήρης σημασία του εκτιμήθηκε μόνο αρκετά χρόνια αργότερα.

Κβαντική θεωρία του φωτός

Αποδεικνύεται ότι τα ηλεκτρόνια μετατοπίζονται από το φωτοηλεκτρικό φαινόμενο εάν το φως φτάσει σε μια συχνότητα κατωφλίου. Κάτω από αυτή τη συχνότητα δεν μπορούν να εκπέμπονται ηλεκτρόνια από το μέταλλο. Το 1905 ο Άλμπερτ Αϊνστάιν δημοσίευσε μια εργασία που εξηγούσε το φαινόμενο. Ο Αϊνστάιν πρότεινε ότι μια δέσμη φωτός δεν είναι ένα κύμα που διαδίδεται στο χώρο, αλλά μάλλον μια συλλογή από διακριτά πακέτα κύματος (φωτόνια), το καθένα με ενέργεια. Ο Αϊνστάιν είπε ότι το φαινόμενο οφειλόταν σε ένα φωτόνιο που χτυπούσε ένα ηλεκτρόνιο. Αυτό απέδειξε τη σωματιδιακή φύση του φωτός.

Ο Αϊνστάιν διαπίστωσε επίσης ότι η ηλεκτρομαγνητική ακτινοβολία με μεγάλο μήκος κύματος δεν είχε καμία επίδραση. Ο Αϊνστάιν είπε ότι αυτό συνέβαινε επειδή τα "σωματίδια" δεν είχαν αρκετή ενέργεια για να διαταράξουν τα ηλεκτρόνια.

Ο Plank πρότεινε ότι η ενέργεια κάθε φωτονίου σχετίζεται με τη συχνότητα του φωτονίου μέσω της σταθεράς του Planck. Αυτό μπορεί να γραφτεί μαθηματικά ως εξής:

E = h ν = h c λ {\displaystyle E=h\nu ={\frac {hc}{\lambda }}}.

Ο Πλανκ έλαβε το βραβείο Νόμπελ το 1918 σε αναγνώριση των υπηρεσιών που προσέφερε στην πρόοδο της Φυσικής με την ανακάλυψη των κβάντα ενέργειας. Το 1921 ο Αϊνστάιν έλαβε το βραβείο Νόμπελ για τη σύνδεση της σταθεράς του Πλανκ με το φωτοηλεκτρικό φαινόμενο.

Απεικόνιση από την πρωτότυπη επιστολή του Νεύτωνα προς τη Βασιλική Εταιρεία (1 Ιανουαρίου 1671 [Ιουλιανό ημερολόγιο]). Το S αντιπροσωπεύει το ηλιακό φως. Το φως μεταξύ των επιπέδων BC και DE είναι έγχρωμο. Αυτά τα χρώματα ανασυνδυάζονται για να σχηματίσουν το ηλιακό φως στο επίπεδο GH


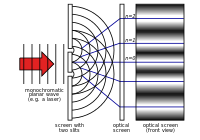
Το πείραμα διπλής σχισμής του Young


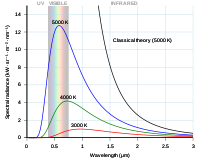
Καμπύλη Rayleigh-Jeans και καμπύλη Planck σε συνάρτηση με το μήκος κύματος των φωτονίων.


Συνέδριο Solway 1911. Οι Planck, Einstein και Jeans στέκονται όρθιοι. Ο Planck είναι δεύτερος από αριστερά. Ο Αϊνστάιν είναι δεύτερος από δεξιά. Ο Τζινς είναι πέμπτος από δεξιά. Ο Wien κάθεται, τρίτος από δεξιά.

Εφαρμογή

Η σταθερά του Planck είναι σημαντική σε πολλές εφαρμογές. Μερικές από αυτές παρατίθενται παρακάτω.

Το μοντέλο Bohr του ατόμου

Το 1913 ο Niels Bohr δημοσίευσε το μοντέλο Bohr για τη δομή του ατόμου. Ο Bohr είπε ότι η στροφορμή των ηλεκτρονίων που κινούνται γύρω από τον πυρήνα μπορεί να έχει μόνο ορισμένες τιμές. Οι τιμές αυτές δίνονται από την εξίσωση

L = n h 2 π {\displaystyle L=n{\frac {h}{2\pi }}}

όπου

L = στροφορμή που συνδέεται με ένα επίπεδο.

n = θετικός ακέραιος αριθμός.

h = σταθερά του Planck.

Το μοντέλο Bohr του ατόμου μπορεί να χρησιμοποιηθεί για τον υπολογισμό της ενέργειας των ηλεκτρονίων σε κάθε επίπεδο. Τα ηλεκτρόνια θα γεμίσουν κανονικά τις χαμηλότερες αριθμημένες καταστάσεις ενός ατόμου. Εάν το άτομο λάβει ενέργεια από, για παράδειγμα, ένα ηλεκτρικό ρεύμα, τα ηλεκτρόνια θα διεγερθούν σε μια υψηλότερη κατάσταση. Στη συνέχεια, τα ηλεκτρόνια θα επιστρέψουν σε μια χαμηλότερη κατάσταση και θα χάσουν την επιπλέον ενέργειά τους εκπέμποντας ένα φωτόνιο. Επειδή οι ενεργειακές στάθμες έχουν συγκεκριμένες τιμές, τα φωτόνια θα έχουν συγκεκριμένες ενεργειακές στάθμες. Το φως που εκπέμπεται με αυτόν τον τρόπο μπορεί να χωριστεί σε διαφορετικά χρώματα χρησιμοποιώντας ένα πρίσμα. Κάθε στοιχείο έχει το δικό του μοτίβο. Το μοτίβο για το νέον παρουσιάζεται παραπλεύρως.

Η αρχή της αβεβαιότητας του Χάιζενμπεργκ

Το 1927 ο Βέρνερ Χάιζενμπεργκ δημοσίευσε την αρχή της αβεβαιότητας. Η αρχή δηλώνει ότι δεν είναι δυνατόν να γίνει μια μέτρηση χωρίς να διαταραχθεί το μετρούμενο πράγμα. Θέτει επίσης ένα όριο στην ελάχιστη διαταραχή που προκαλείται από την πραγματοποίηση μιας μέτρησης.

Στον μακροσκοπικό κόσμο αυτές οι διαταραχές κάνουν πολύ μικρή διαφορά. Για παράδειγμα, αν μετρηθεί η θερμοκρασία μιας φιάλης με υγρό, το θερμόμετρο θα απορροφήσει ένα μικρό ποσό ενέργειας καθώς θερμαίνεται. Αυτό θα προκαλέσει ένα μικρό σφάλμα στην τελική ένδειξη, αλλά το σφάλμα αυτό είναι μικρό και δεν έχει σημασία.

Στην κβαντομηχανική τα πράγματα είναι διαφορετικά. Ορισμένες μετρήσεις γίνονται με την εξέταση του μοτίβου των σκεδαζόμενων φωτονίων. Ένα τέτοιο παράδειγμα είναι η σκέδαση Compton. Εάν μετράται τόσο η θέση όσο και η ορμή ενός σωματιδίου, η αρχή της αβεβαιότητας δηλώνει ότι υπάρχει συμβιβασμός μεταξύ της ακρίβειας με την οποία μετράται η ορμή και της ακρίβειας με την οποία μετράται η θέση. Η εξίσωση που περιγράφει αυτή την αντιστάθμιση είναι η εξής:

Δ x Δ p ≳ h {\displaystyle \Delta x\,\Delta p\gtrsim h\qquad \qquad \qquad \qquad }

όπου

Δp = αβεβαιότητα στην ορμή.

Δx = αβεβαιότητα θέσης.

h = σταθερά του Planck.

Χρώμα διόδων εκπομπής φωτός

Στο ηλεκτρικό κύκλωμα που παρουσιάζεται στα δεξιά, η πτώση τάσης στην δίοδο εκπομπής φωτός (LED) εξαρτάται από το υλικό της LED. Για τις διόδους πυριτίου η πτώση είναι 0,6 V. Ωστόσο, για τις λυχνίες LED κυμαίνεται μεταξύ 1,8 V και 2,7 V. Η πληροφορία αυτή επιτρέπει σε έναν χρήστη να υπολογίσει τη σταθερά του Planck.

Η ενέργεια που χρειάζεται ένα ηλεκτρόνιο για να υπερπηδήσει το φράγμα δυναμικού στο υλικό LED δίνεται από τη σχέση

E = Q e V L {\displaystyle E=Q_{e}V_{L}\,}

όπου

Q_e είναι το φορτίο ενός ηλεκτρονίου.

V_L είναι η πτώση τάσης στο LED.

Όταν το ηλεκτρόνιο διασπάται και πάλι, εκπέμπει ένα φωτόνιο φωτός. Η ενέργεια του φωτονίου δίνεται από την ίδια εξίσωση που χρησιμοποιείται στο φωτοηλεκτρικό φαινόμενο. Αν οι εξισώσεις αυτές συνδυαστούν, το μήκος κύματος του φωτός και η τάση συνδέονται με τη σχέση

λ = h c V L Q e {\displaystyle \lambda ={\frac {hc}{V_{L}Q_{e}}}\,}

Από τη σχέση αυτή μπορεί να υπολογιστεί ο παρακάτω πίνακας.

Χρώμα	Μήκος κύματος (nm)	Τάση
κόκκινο φως	650	1.89
πράσινο φως	550	2.25
μπλε φως	470	2.62

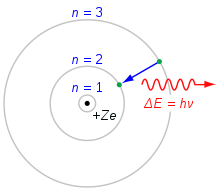
Το μοντέλο του ατόμου του Bohr. Ένα ηλεκτρόνιο που πέφτει από το κέλυφος n=3 στο κέλυφος n=2 χάνει ενέργεια. Η ενέργεια αυτή μεταφέρεται ως ένα φωτόνιο.


Ορατό φάσμα του Νέον. Κάθε γραμμή αντιπροσωπεύει ένα διαφορετικό ζεύγος ενεργειακών επιπέδων.


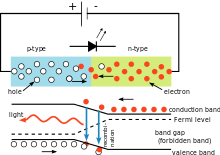
Απλό κύκλωμα LED που απεικονίζει τη χρήση της σταθεράς του Planck. Το χρώμα του εκπεμπόμενου φωτός εξαρτάται από την πτώση τάσης στη δίοδο. Το μήκος κύματος του φωτός μπορεί να υπολογιστεί χρησιμοποιώντας τη σταθερά του Planck.

Τιμή της σταθεράς του Planck και επαναπροσδιορισμός του χιλιόγραμμου

Από την ανακάλυψή του, οι μετρήσεις του h έχουν γίνει πολύ καλύτερες. Ο Planck ανέφερε για πρώτη φορά την τιμή του h σε 6,55×10 ⁻²⁷erg-sec. Αυτή η τιμή είναι μέσα στο 5% της τρέχουσας τιμής.

Από τις 3 Μαρτίου 2014, οι καλύτερες μετρήσεις του h σε μονάδες SI είναι 6,62606957×10 ⁻³⁴J-s. Η ισοδύναμη τιμή σε μονάδες cgs είναι 6,62606957×10 ⁻²⁷erg-sec. Η σχετική αβεβαιότητα του h είναι 4,4×10 . ⁻⁸

Η μειωμένη σταθερά του Planck (ħ) είναι μια τιμή που χρησιμοποιείται μερικές φορές στην κβαντομηχανική. Ορίζεται από τη σχέση

ℏ = h 2 π {\displaystyle \hbar ={\frac {h}{2\pi }}}.

Οι μονάδες Planck χρησιμοποιούνται μερικές φορές στην κβαντομηχανική αντί του SI. Σε αυτό το σύστημα η μειωμένη σταθερά Planck έχει τιμή 1, οπότε η τιμή της σταθεράς Planck είναι 2π.

Η σταθερά Plancks μπορεί πλέον να μετρηθεί με πολύ υψηλή ακρίβεια. Αυτό έκανε το BIPM να εξετάσει έναν νέο ορισμό για το χιλιόγραμμο. Το διεθνές πρωτότυπο χιλιόγραμμο δεν χρησιμοποιείται πλέον για τον ορισμό του χιλιόγραμμου. Αντ' αυτού, το BIPM ορίζει τη σταθερά του Planck να έχει ακριβή τιμή. Οι επιστήμονες χρησιμοποιούν αυτή την τιμή και τους ορισμούς του μέτρου και του δευτερολέπτου για να ορίσουν το χιλιόγραμμο.

 

Τιμή της θεωρητικής σταθεράς Planck

Η σταθερά του Planck μπορεί επίσης να προκύψει μαθηματικά:

 

h = μ 0 π 12 c 3 [ q 0 [ 0.9163 a 0 ] 2 ] 2 f 1 r 5 ⋅ s = 6.63 × 10 - 34 J ⋅ s {\displaystyle h={\frac {\mu _{0}\pi }{12c^{3}}}{[{q_{0}}}{[0.9163a_{0}]}^{2}]^{2}}}{f_{1r}}}^{5}\cdot {s}=6.63\times 10^{-34}J\cdot s}

Εδώ, μ 0 {\displaystyle \mu _{0}} είναι η διαπερατότητα του ελεύθερου χώρου, c {\displaystyle c} είναι η ταχύτητα του φωτός, q 0 {\displaystyle q_{0}} είναι το ηλεκτρικό φορτίο του ηλεκτρονίου, a 0 {\displaystyle a_{0}} είναι η ακτίνα του Bohr και f 1 r {\displaystyle f_{1r}} είναι η συχνότητα περιστροφής του ηλεκτρονίου σε ένα άτομο υδρογόνου ( f 1 r = 3.29 × 10 15 r e v / s ) {\displaystyle (f_{1r}=3.29\times 10^{15}rev/s)} . Όταν αυτές οι σταθερές τιμές αντικαθίστανται στη θεωρητική σταθερά Planck, η θεωρητική τιμή της σταθεράς Planck είναι ακριβώς ίση με την πειραματική τιμή.

Σχετικές σελίδες

• Δυαδικότητα κύματος-σωματιδίου