Στοιχειώδης άλγεβρα

Η στοιχειώδης άλγεβρα είναι η πιο βασική μορφή άλγεβρας που διδάσκεται στους μαθητές. Συχνά είναι ένας από τους επόμενους τομείς των μαθηματικών που διδάσκονται στους μαθητές μετά την αριθμητική. Ενώ στην αριθμητική εμφανίζονται μόνο αριθμοί και τελεστές όπως +, -, × και ÷, στην άλγεβρα χρησιμοποιούνται μεταβλητές (όπως a, x, y) για να αντιπροσωπεύουν αριθμούς. Αυτό είναι χρήσιμο επειδή:

Επιτρέπει στους ανθρώπους να λύνουν προβλήματα σχετικά με "άγνωστους" αριθμούς. Αυτό σημαίνει ότι μαθαίνουν για τις εξισώσεις και πώς να τις λύνουν (για παράδειγμα, "βρείτε έναν αριθμό x όπου 3 x + 1 = 10 {\displaystyle 3x+1=10} $3x+1=10$ ").
Επιτρέπει τη γενίκευση των κανόνων της αριθμητικής. Ενώ κάποιοι μαθητές καταλαβαίνουν ότι 3 + 4 = 4 + 3 {\displaystyle 3+4=4+3} $3+4=4+3$ , βοηθά να αποδείξουν ότι a + b = b + a {\displaystyle a+b=b+a} για όλα τα a και b. Αυτό κάνει την άλγεβρα ένα καλό βήμα για την εκμάθηση της αφαίρεσης (εκμάθηση γενικών ιδεών από πολλά παραδείγματα).
Βοηθά τους ανθρώπους να κατανοήσουν και να δημιουργήσουν λειτουργικές σχέσεις (που μερικές φορές αποκαλούνται επίσης αιτία και αποτέλεσμα). Ένα παράδειγμα είναι "αν πωληθούν x εισιτήρια, τότε το κέρδος θα είναι 3 x - 10 {\displaystyle 3x-10} $3x-10$ δολάρια".

Αυτά τα τρία είναι τα κύρια σκέλη της στοιχειώδους άλγεβρας. Η στοιχειώδης άλγεβρα χρησιμοποιείται συχνά σε πολλά άλλα θέματα, όπως η επιστήμη, οι επιχειρήσεις και η οικοδομή. Η αφηρημένη άλγεβρα, ένα πολύ πιο προχωρημένο θέμα, διδάσκεται γενικά αργά στο κολέγιο.

Απλά προβλήματα άλγεβρας

Αν μια εξίσωση έχει μόνο έναν άγνωστο αριθμό, είναι μερικές φορές εύκολο να λυθεί. Ο άγνωστος αριθμός ονομάζεται "x":

2 x + 4 = 12. {\displaystyle 2x+4=12.\,} $2x+4=12.\,$

Για την επίλυση μιας απλής εξίσωσης με ένα άγνωστο ποσό προσθέστε, αφαιρέστε, πολλαπλασιάστε ή διαιρέστε και τις δύο πλευρές της εξίσωσης με τον ίδιο αριθμό ώστε να τοποθετήσετε το άγνωστο ποσό, x, στη μία πλευρά της εξίσωσης. Μόλις το x βρεθεί μόνο του στη μία πλευρά, χρησιμοποιήστε την αριθμητική για να προσδιορίσετε το ποσό στην άλλη πλευρά της εξίσωσης. Για παράδειγμα, αφαιρώντας 4 και από τις δύο πλευρές της παραπάνω εξίσωσης:

2 x + 4 - 4 = 12 - 4 {\displaystyle 2x+4-4-4=12-4\,} $2x+4-4=12-4\,$

να πάρει:

2 x = 8 {\displaystyle 2x=8\,} $2x=8\,$

Διαιρώντας και τις δύο πλευρές με το 2:

2 x 2 = 8 2 {\displaystyle {\frac {2x}{2}}={\frac {8}{2}}\,} ${\frac {2x}{2}}={\frac {8}{2}}\,$

να πάρει:

x = 4. {\displaystyle x=4.\,} $x=4.\,$

Μπορεί να σας βοηθήσει να σκεφτείτε αυτή την εξίσωση ως μια σβούρα ή ισορροπία, ό,τι κάνετε στη μία πλευρά, πρέπει να κάνετε και στην άλλη και ο κύριος στόχος σας είναι να πάρετε το x από μόνο του.

Ορισμοί

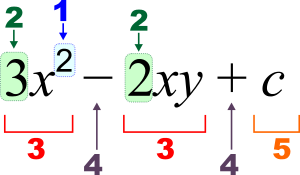
3 x 2 - 2 x y + c {\displaystyle 3x^{2}-2xy+c} $3x^{2}-2xy+c$ έχει τις ακόλουθες συνιστώσες:

1 : Εκθέτης (δύναμη), 2 : Συντελεστής, 3 : όρος, 4 : τελεστής, 5 : σταθερά, x , y {\displaystyle x,y} : $x,y$ μεταβλητές

Ερωτήσεις και απαντήσεις

Q: Τι είναι η στοιχειώδης άλγεβρα;

Α: Η στοιχειώδης άλγεβρα είναι η πιο βασική μορφή άλγεβρας που διδάσκεται στους μαθητές. Συνήθως ακολουθεί την αριθμητική και περιλαμβάνει τη χρήση μεταβλητών (όπως a, x, y) για να αντιπροσωπεύουν αριθμούς σε εξισώσεις.

Ε: Ποιες είναι ορισμένες χρήσεις της στοιχειώδους άλγεβρας;

Α: Η στοιχειώδης άλγεβρα μπορεί να χρησιμοποιηθεί για την επίλυση προβλημάτων σχετικά με άγνωστους αριθμούς, τη γενίκευση κανόνων από την αριθμητική, την κατανόηση και τη δημιουργία λειτουργικών σχέσεων και χρησιμοποιείται συχνά σε πολλά άλλα μαθήματα όπως η επιστήμη, οι επιχειρήσεις και η οικοδομή.

Ερ: Πώς η στοιχειώδης άλγεβρα βοηθά τους ανθρώπους να κατανοήσουν αφηρημένες ιδέες;

Α: Η στοιχειώδης άλγεβρα βοηθά τους ανθρώπους να μάθουν γενικές ιδέες από πολλά παραδείγματα αποδεικνύοντας ότι a+b=b+a για όλα τα a και b. Αυτό τους επιτρέπει να κατανοήσουν καλύτερα τις αφηρημένες έννοιες.

Ερ: Είναι η αφηρημένη άλγεβρα πιο προχωρημένη από τη στοιχειώδη άλγεβρα;

Α: Ναι, η αφηρημένη άλγεβρα διδάσκεται γενικά αργά στο κολέγιο και είναι πολύ πιο προχωρημένη από τη στοιχειώδη άλγεβρα.

Ερ: Τι είδους εξισώσεις περιλαμβάνει η στοιχειώδης άλγεβρα;

Α: Η στοιχειώδης άλγεβρα περιλαμβάνει εξισώσεις με μεταβλητές (όπως a, x, y) που αντιπροσωπεύουν αριθμούς καθώς και τελεστές όπως +,- ,× ,και ÷ .
3x+1=10 {\displaystyle 3x+1=10}

Ερ: Πώς μπορεί η κατανόηση της στοιχειώδους άλγεβρας να βοηθήσει σε άλλα μαθήματα;

Α: Η κατανόηση της στοιχειώδους Άλγεβρας μπορεί να βοηθήσει σε άλλα μαθήματα όπως η επιστήμη, οι επιχειρήσεις ή η οικοδομή, καθώς επιτρέπει στους ανθρώπους να λύνουν προβλήματα σχετικά με άγνωστους αριθμούς και να δημιουργούν λειτουργικές σχέσεις μεταξύ διαφορετικών μεταβλητών.