Πολλαπλασιασμός
Ο πολλαπλασιασμός είναι μια αριθμητική πράξη για την εύρεση του γινομένου δύο αριθμών. Ο πολλαπλασιασμός είναι η τρίτη πράξη στα μαθηματικά μετά την πρόσθεση που είναι η πρώτη, την αφαίρεση που είναι η δεύτερη και μετά υπάρχει ο πολλαπλασιασμός.
Με τους φυσικούς αριθμούς, σας λέει τον αριθμό των πλακιδίων σε ένα ορθογώνιο όπου ένας από τους δύο αριθμούς ισούται με τον αριθμό των πλακιδίων στη μία πλευρά και ο άλλος αριθμός ισούται με τον αριθμό των πλακιδίων στην άλλη πλευρά.
Με πραγματικούς αριθμούς, σας λέει το εμβαδόν ενός ορθογωνίου όπου ο πρώτος αριθμός ισούται με το μέγεθος της μιας πλευράς και ο δεύτερος αριθμός ισούται με το μέγεθος της άλλης πλευράς.
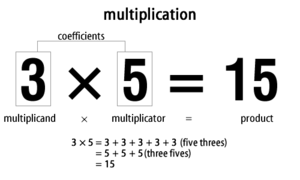
Για παράδειγμα, το τρία πολλαπλασιασμένο με το πέντε είναι το σύνολο των πέντε τριάδων που προστίθενται ή το σύνολο των τριών πεντάδων. Αυτό μπορεί να γραφτεί ως 3 × 5 = 15, ή να ειπωθεί ως "τρεις φορές το πέντε ισούται με δεκαπέντε". Οι μαθηματικοί αποκαλούν τους δύο αριθμούς που θέλετε να πολλαπλασιάσετε "συντελεστές" μαζί, ή "πολλαπλασιαστή" και "πολλαπλασιαστή" ξεχωριστά. Πολλαπλασιαστής × πολλαπλασιαστής = γινόμενο.
Ο πολλαπλασιασμός μεταξύ αριθμών λέγεται αντιμεταθετικός - όταν η σειρά των αριθμών δεν επηρεάζει την τιμή του γινομένου. Αυτό ισχύει για τους ακέραιους αριθμούς (ακέραιοι αριθμοί), π.χ. 4 × 6 είναι το ίδιο με 6 × 4, και επίσης για τους ορθολογικούς αριθμούς (κλάσματα), και για όλους τους άλλους πραγματικούς αριθμούς (που μπορούν να αναπαρασταθούν ως πεδίο στη συνεχή γραμμή), και επίσης για τους μιγαδικούς αριθμούς (αριθμοί που μπορούν να αναπαρασταθούν ως πεδίο στο επίπεδο). Δεν ισχύει για τα τεταρτημόρια (αριθμοί που μπορούν να αναπαρασταθούν ως δακτύλιος στον τετραδιάστατο χώρο), τα διανύσματα ή τους πίνακες.
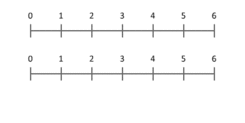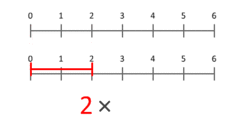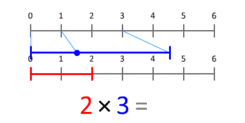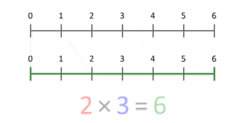
Ο ορισμός του πολλαπλασιασμού ως επαναλαμβανόμενη πρόσθεση παρέχει έναν τρόπο για να καταλήξουμε σε μια θεωρητική ερμηνεία του πολλαπλασιασμού των καρδιακών αριθμών. Μια πιο ακριβής αναπαράσταση είναι να τον θεωρήσουμε ως κλιμάκωση ποσοτήτων. Αυτό το κινούμενο σχέδιο απεικονίζει τον πολλαπλασιασμό του 3 με το 2, δίνοντας ως αποτέλεσμα το 6. Παρατηρήστε ότι η μπλε κουκκίδα στο μπλε τμήμα μήκους 3 τοποθετείται στη θέση 1, και το μπλε τμήμα κλιμακώνεται έτσι ώστε η κουκκίδα αυτή να τοποθετείται στο τέλος του κόκκινου τμήματος, μήκους 2. Για πολλαπλασιασμό με οποιοδήποτε X, η μπλε κουκκίδα θα ξεκινά πάντα από το 1 και θα καταλήγει στο X. Αυτό λειτουργεί ακόμη και για X μικρότερο από 1, ή αρνητικό.
Το αντίθετο του πολλαπλασιασμού είναι η διαίρεση.
Πίνακας πολλαπλασιασμού
Οι δάσκαλοι συνήθως απαιτούν από τους μαθητές τους να απομνημονεύσουν τον πίνακα των πρώτων 9 αριθμών όταν διδάσκουν τον πολλαπλασιασμό.
| Πίνακας των 6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Πίνακας πολλαπλασιασμού | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Σχετικές σελίδες
- Προσθήκη
- Τετραγωνικός αριθμός
- Αφαίρεση
Ερωτήσεις και απαντήσεις
Q: Τι είναι ο πολλαπλασιασμός;
Α: Ο πολλαπλασιασμός είναι μια αριθμητική πράξη για την εύρεση του γινομένου δύο αριθμών στα μαθηματικά. Συχνά αναπαρίσταται με σύμβολα όπως × και ⋅.
Ερ: Πώς ονομάζονται οι δύο αριθμοί που πρέπει να πολλαπλασιαστούν;
Α: Οι δύο αριθμοί που πρόκειται να πολλαπλασιαστούν αναφέρονται ως "συντελεστές" ή "πολλαπλασιαστή" και "πολλαπλασιαστή" ξεχωριστά.
Ερ: Είναι ο πολλαπλασιασμός αντιμεταθετικός;
Α: Ναι, ο πολλαπλασιασμός μεταξύ αριθμών λέγεται αντιμεταθετικός - όταν η σειρά των αριθμών δεν επηρεάζει την τιμή του γινομένου. Αυτό ισχύει για ακέραιους, ορθολογικούς, πραγματικούς και μιγαδικούς αριθμούς. Ωστόσο, δεν ισχύει για τα quaternions, τα διανύσματα ή τους πίνακες.
Ερ: Πώς μπορούμε να ερμηνεύσουμε τον πολλαπλασιασμό των καρδιακών αριθμών;
Α: Μπορούμε να ερμηνεύσουμε τον πολλαπλασιασμό των καρδιακών αριθμών ως μεγέθη κλίμακας - όταν ένας αριθμός (ο πολλαπλασιαστής) κλιμακώνεται έτσι ώστε μια τελεία που τοποθετείται στη θέση 1 να καταλήγει σε ένα συγκεκριμένο σημείο (ο πολλαπλασιαστής).
Ερώτηση: Πώς αναπαριστάτε το τρία πολλαπλασιασμένο με το πέντε;
Α: Το τρία πολλαπλασιασμένο επί πέντε μπορεί να γραφτεί ως 3 × 5 = 15, ή να ειπωθεί ως "τρεις φορές το πέντε ισούται με δεκαπέντε".
Ερ: Ποιο είναι το αντίθετο του πολλαπλασιασμού;
Α: Το αντίθετο του πολλαπλασιασμού είναι η διαίρεση.
ψάχνω