Μετασχηματισμός Φουριέ
Ο μετασχηματισμός Fourier είναι μια μαθηματική συνάρτηση που μπορεί να χρησιμοποιηθεί για την εύρεση των βασικών συχνοτήτων που συνθέτουν ένα σήμα ή κύμα. Για παράδειγμα, εάν παίζεται μια συγχορδία, το ηχητικό κύμα της συγχορδίας μπορεί να εισαχθεί σε έναν μετασχηματισμό Fourier για να βρεθούν οι νότες από τις οποίες αποτελείται η συγχορδία. Η έξοδος ενός μετασχηματισμού Fourier ονομάζεται μερικές φορές φάσμα συχνοτήτων ή κατανομή, επειδή εμφανίζει ένα φάσμα των συχνοτήτων της εισόδου. Αυτή η λειτουργία έχει πολλές χρήσεις στην κρυπτογραφία, την ωκεανογραφία, τη μηχανική μάθηση, την ακτινολογία, την κβαντική φυσική καθώς και στον σχεδιασμό και την οπτικοποίηση ήχου.
Ο μετασχηματισμός Fourier μιας συνάρτησης f ( x ) {\displaystyle f(x)}
F ( α ) = ∫ - ∞ + ∞ f ( x ) e - 2 π i α x d x {\displaystyle F(\alpha )=\int _{-\infty }^{+\infty }f(x)e^{-2\pi i\alpha x}dx}}
α {\displaystyle \alpha } 
F ( α ) {\displaystyle F(\alpha )} 

e - 2 π i α x {\displaystyle e^{-2\pi i\alpha x}} 

Ο αντίστροφος μετασχηματισμός Fourier δίνεται από τη σχέση
f ( x ) = ∫ - ∞ + ∞ F ( α ) e + 2 π i x α d α {\displaystyle f(x)=\int _{-\infty }^{+\infty }F(\alpha )e^{+2\pi ix\alpha }d\alpha }
Ο μετασχηματισμός Fourier δείχνει ποιες συχνότητες υπάρχουν σε ένα σήμα. Για παράδειγμα, θεωρήστε ένα ηχητικό κύμα που περιέχει τρεις διαφορετικές μουσικές νότες: Κάνοντας μια γραφική παράσταση του μετασχηματισμού Fourier αυτού του ηχητικού κύματος (με τη συχνότητα στον άξονα x και την ένταση στον άξονα y) θα δούμε μια κορυφή σε κάθε συχνότητα που αντιστοιχεί σε μια από τις μουσικές νότες.
Πολλά σήματα μπορούν να δημιουργηθούν με την πρόσθεση συνημιτόνων και ημιτόνων με διαφορετικά πλάτη και συχνότητες. Ο μετασχηματισμός Fourier απεικονίζει τα πλάτη και τις φάσεις αυτών των συνημιτόνων και ημιτόνων συναρτήσει των αντίστοιχων συχνοτήτων τους.
Οι μετασχηματισμοί Fourier είναι σημαντικοί επειδή πολλά σήματα έχουν περισσότερο νόημα όταν οι συχνότητές τους διαχωρίζονται. Στο παραπάνω παράδειγμα ήχου, η εξέταση του σήματος σε σχέση με το χρόνο δεν καθιστά προφανές ότι οι νότες A, B και C βρίσκονται στο σήμα. Πολλά συστήματα κάνουν διαφορετικά πράγματα σε διαφορετικές συχνότητες, οπότε αυτού του είδους τα συστήματα μπορούν να περιγραφούν από το τι κάνουν σε κάθε συχνότητα. Ένα παράδειγμα είναι ένα φίλτρο που εμποδίζει τις υψηλές συχνότητες.
Ο υπολογισμός ενός μετασχηματισμού Fourier απαιτεί κατανόηση της ολοκλήρωσης και των φανταστικών αριθμών. Οι υπολογιστές χρησιμοποιούνται συνήθως για τον υπολογισμό μετασχηματισμών Fourier για οτιδήποτε άλλο εκτός από τα πιο απλά σήματα. Ο γρήγορος μετασχηματισμός Fourier είναι μια μέθοδος που χρησιμοποιούν οι υπολογιστές για τον γρήγορο υπολογισμό ενός μετασχηματισμού Fourier.
· 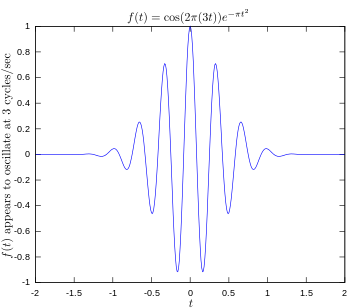
Αρχική συνάρτηση που δείχνει ένα σήμα που ταλαντώνεται στα 3 hertz.
· 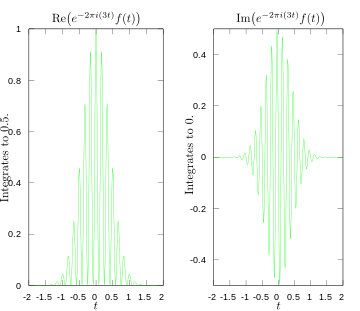
Πραγματικό και φανταστικό μέρος του ολοκληρώματος για μετασχηματισμό Fourier στα 3 hertz
· 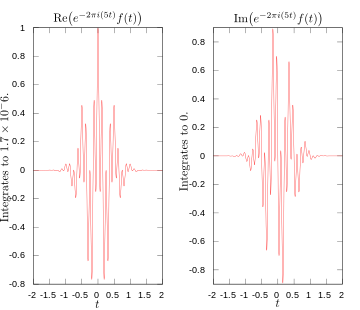
Πραγματικό και φανταστικό μέρος του ολοκληρώματος για μετασχηματισμό Fourier στα 5 hertz
· 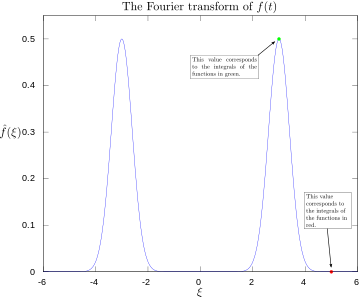
Μετασχηματισμός Fourier με 3 και 5 hertz επισημασμένα.
Ερωτήσεις και απαντήσεις
Ερ: Τι είναι ο μετασχηματισμός Fourier;
A: Ο μετασχηματισμός Fourier είναι μια μαθηματική συνάρτηση που μπορεί να χρησιμοποιηθεί για να βρεθούν οι βασικές συχνότητες από τις οποίες αποτελείται ένα κύμα. Παίρνει ένα σύνθετο κύμα και βρίσκει τις συχνότητες που το συνθέτουν, επιτρέποντάς του να προσδιορίσει τις νότες που συνθέτουν μια συγχορδία.
Ερ: Ποιες είναι ορισμένες χρήσεις του μετασχηματισμού Fourier;
Α: Ο μετασχηματισμός Fourier έχει πολλές χρήσεις στην κρυπτογραφία, την ωκεανογραφία, τη μηχανική μάθηση, την ακτινολογία, την κβαντική φυσική καθώς και στον σχεδιασμό και την οπτικοποίηση του ήχου.
Ερ: Πώς υπολογίζεται ο μετασχηματισμός Fourier;
A: Ο μετασχηματισμός Fourier μιας συνάρτησης f(x) δίνεται από τη σχέση: F(ב) = ∫-∞+∞f(x)e-2נiבxdx όπου ב είναι μια συχνότητα. Αυτό επιστρέφει μια τιμή που αντιπροσωπεύει πόσο διαδεδομένη είναι η συχνότητα ב στο αρχικό σήμα. Ο αντίστροφος μετασχηματισμός Fourier δίνεται από τη σχέση: f(x) = ∫-∞+∞F(ב)e+2נixבdב.
Ερ: Πώς μοιάζει η έξοδος ενός μετασχηματισμού Fourier;
A: Η έξοδος ενός μετασχηματισμού Fourier μπορεί να ονομαστεί είτε φάσμα συχνοτήτων είτε κατανομή, επειδή εμφανίζει μια κατανομή των πιθανών συχνοτήτων της εισόδου.
Ερ: Πώς υπολογίζουν οι υπολογιστές τους γρήγορους μετασχηματισμούς Fourier;
Α: Οι υπολογιστές χρησιμοποιούν έναν αλγόριθμο που ονομάζεται Γρήγορος Μετασχηματισμός Fourier (Fast Fourier Transform - FFT) για να υπολογίζουν γρήγορα τους μετασχηματισμούς οποιουδήποτε σήματος εκτός από τους απλούστερους.
Ερ: Τι δεν μας δείχνει η εξέταση των σημάτων σε σχέση με το χρόνο;
Α: Η εξέταση των σημάτων σε σχέση με το χρόνο δεν καθιστά προφανές ποιες νότες υπάρχουν σε αυτά- πολλά σήματα αποκτούν περισσότερο νόημα όταν οι συχνότητές τους διαχωρίζονται και αναλύονται ξεχωριστά αντ' αυτού.
ψάχνω

