Λογαριθμική κλίμακα
Η λογαριθμική κλίμακα είναι μια κλίμακα που χρησιμοποιείται όταν υπάρχει μεγάλο εύρος ποσοτήτων. Οι συνήθεις χρήσεις περιλαμβάνουν την ισχύ του σεισμού, την ένταση του ήχου, την ένταση του φωτός και το pH των διαλυμάτων.
Βασίζεται σε τάξεις μεγέθους και όχι σε μια τυπική γραμμική κλίμακα. Η τιμή κάθε σημείου στην κλίμακα είναι η τιμή στο προηγούμενο σημείο πολλαπλασιασμένη με μια σταθερά.
Οι λογαριθμικές κλίμακες χρησιμοποιούνται επίσης στους διαβήτες για τον πολλαπλασιασμό ή τη διαίρεση αριθμών με την πρόσθεση ή την αφαίρεση μηκών στις κλίμακες.
Η λογαριθμική κλίμακα μπορεί να είναι χρήσιμη όταν τα δεδομένα καλύπτουν ένα μεγάλο εύρος τιμών - ο λογάριθμος το μειώνει σε ένα πιο εύχρηστο εύρος.
Ορισμένες από τις αισθήσεις μας λειτουργούν με λογαριθμικό τρόπο (ο πολλαπλασιασμός της πραγματικής ισχύος εισόδου προσθέτει μια σταθερά στην αντιληπτή ισχύ του σήματος, βλ: νόμος ισχύος του Stevens). Αυτό καθιστά τις λογαριθμικές κλίμακες για αυτές τις ποσότητες εισόδου ιδιαίτερα κατάλληλες. Ειδικότερα, η αίσθηση της ακοής μας αντιλαμβάνεται ίσα πολλαπλάσια των συχνοτήτων ως ίσες διαφορές στον τόνο.
Στις περισσότερες λογαριθμικές κλίμακες, τα μικρά πολλαπλάσια (ή αναλογίες) της υποκείμενης ποσότητας αντιστοιχούν σε μικρές (ενδεχομένως αρνητικές) τιμές του λογαριθμικού μέτρου.
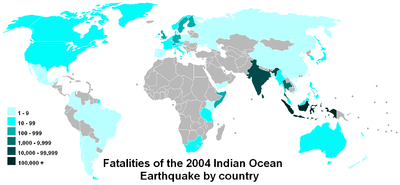
Η κλίμακα λογαρίθμου διευκολύνει τη σύγκριση τιμών που καλύπτουν ένα μεγάλο εύρος, όπως σε αυτόν τον χάρτη
Οι δύο λογαριθμικές κλίμακες ενός κανόνα διαφάνειας
Παραδείγματα
Γνωστά παραδείγματα τέτοιων κλιμάκων είναι:
- Κλίμακα μεγέθους Richter και κλίμακα μεγέθους ροπής (MMS) για την ένταση των σεισμών και την κίνηση στη γη.
- bel και decibel και neper για την ακουστική ισχύ (ένταση) και την ηλεκτρική ισχύ,
- καταμέτρηση των f-stops για τις αναλογίες της φωτογραφικής έκθεσης,
- βαθμολόγηση των χαμηλών πιθανοτήτων με τον αριθμό των "εννιάδων" στο δεκαδικό ανάπτυγμα της πιθανότητας να μην συμβεί: για παράδειγμα, ένα σύστημα που θα αποτύχει με πιθανότητα 10−5είναι 99,999% αξιόπιστο: "πέντε εννιάρια".
- Εντροπία στη θερμοδυναμική.
- Η πληροφορία στη θεωρία της πληροφορίας.
- Καμπύλες κοκκομετρικής κατανομής του εδάφους
Ορισμένες λογαριθμικές κλίμακες σχεδιάστηκαν έτσι ώστε μεγάλες τιμές (ή αναλογίες) του υποκείμενου μεγέθους να αντιστοιχούν σε μικρές τιμές του λογαριθμικού μέτρου. Παραδείγματα τέτοιων κλιμάκων είναι:
- pH για την οξύτητα,
- κλίμακα αστρικού μεγέθους για τη φωτεινότητα των αστέρων,
Η λογαριθμική κλίμακα είναι επίσης μια γραφική κλίμακα στη μία ή και στις δύο πλευρές μιας γραφικής παράστασης όπου ένας αριθμός x εκτυπώνεται σε απόσταση c-log(x) από το σημείο που σημειώνεται με τον αριθμό 1. Ένας slide rule έχει λογαριθμικές κλίμακες και τα νομόγραμμα συχνά χρησιμοποιούν λογαριθμικές κλίμακες. Σε μια λογαριθμική κλίμακα μια ίση διαφορά στη τάξη μεγέθους αντιπροσωπεύεται από μια ίση απόσταση. Ο γεωμετρικός μέσος όρος δύο αριθμών βρίσκεται στο μέσο της απόστασης μεταξύ των αριθμών.
Το λογαριθμικό χαρτί γραφικών, πριν από την εμφάνιση των γραφικών υπολογιστών, ήταν ένα βασικό επιστημονικό εργαλείο. Οι γραφικές παραστάσεις σε χαρτί με κλίμακα ενός λογαρίθμου μπορούν να εμφανίσουν εκθετικούς νόμους, και σε χαρτί λογαρίθμου-λογάριθμου τους νόμους δύναμης, ως ευθείες γραμμές (βλ. ημιλογαριθμικό γράφημα, λογαριθμο-λογάριθμο γράφημα).
Ερωτήσεις και απαντήσεις
Ερ: Τι είναι η λογαριθμική κλίμακα;
A: Η λογαριθμική κλίμακα είναι μια κλίμακα που χρησιμοποιείται όταν υπάρχει μεγάλο εύρος ποσοτήτων.
Ερ: Ποια είναι μερικά παραδείγματα πραγμάτων που μπορούν να μετρηθούν σε λογαριθμική κλίμακα;
Α: Η ισχύς του σεισμού, η ένταση του ήχου, η ένταση του φωτός, ο ρυθμός εξάπλωσης επιδημιών και το pH των διαλυμάτων μπορούν να μετρηθούν σε λογαριθμική κλίμακα.
Ερ: Πώς διαφέρει μια λογαριθμική κλίμακα από μια τυπική γραμμική κλίμακα;
Α: Μια λογαριθμική κλίμακα βασίζεται σε τάξεις μεγέθους, αντί για μια τυπική γραμμική κλίμακα. Η τιμή κάθε σημείου στην κλίμακα είναι η τιμή στο προηγούμενο σημείο πολλαπλασιασμένη με μια σταθερά.
Ερ: Ποιο είναι το πλεονέκτημα της χρήσης λογαριθμικής κλίμακας;
Α: Η λογαριθμική κλίμακα μπορεί να μειώσει ένα μεγάλο εύρος τιμών σε ένα πιο εύχρηστο εύρος, το οποίο μπορεί να είναι χρήσιμο όταν πρόκειται για δεδομένα που καλύπτουν ένα μεγάλο εύρος τιμών.
Ερ: Τι είναι ο νόμος ισχύος του Stevens και πώς σχετίζεται με τις λογαριθμικές κλίμακες;
Α: Ο νόμος ισχύος του Stevens περιγράφει πώς ορισμένες από τις αισθήσεις μας λειτουργούν με λογαριθμικό τρόπο, όπου ο πολλαπλασιασμός της πραγματικής ισχύος εισόδου προσθέτει μια σταθερά στην αντιληπτή ισχύ του σήματος. Αυτό καθιστά τις λογαριθμικές κλίμακες για αυτές τις ποσότητες εισόδου ιδιαίτερα κατάλληλες.
Ερ: Γιατί μια λογαριθμική κλίμακα είναι ιδιαίτερα χρήσιμη για τη μέτρηση της ηχητικής έντασης;
Α: Η αίσθηση της ακοής μας αντιλαμβάνεται ίσα πολλαπλάσια των συχνοτήτων ως ίσες διαφορές στο ύψος, οπότε μια λογαριθμική κλίμακα μπορεί να αναπαραστήσει με ακρίβεια αυτή τη σχέση μεταξύ της συχνότητας του ήχου και της αντιλαμβανόμενης έντασης.
Ερ: Ποια είναι η σχέση μεταξύ των μικρών πολλαπλάσιων της υποκείμενης ποσότητας και του λογαριθμικού μέτρου στις περισσότερες λογαριθμικές κλίμακες;
Α: Στις περισσότερες λογαριθμικές κλίμακες, τα μικρά πολλαπλάσια (ή αναλογίες) της υποκείμενης ποσότητας αντιστοιχούν σε μικρές (ενδεχομένως αρνητικές) τιμές του λογαριθμικού μέτρου.
ψάχνω