Διαφανής κανόνας

Βασικές έννοιες

Στην πιο βασική του μορφή, ο slide rule χρησιμοποιεί δύο λογαριθμικές κλίμακες για να επιτρέπει τον γρήγορο πολλαπλασιασμό και τη διαίρεση αριθμών. Αυτές οι συνήθεις πράξεις μπορεί να είναι χρονοβόρες και επιρρεπείς σε σφάλματα όταν γίνονται σε χαρτί. Οι πιο πολύπλοκοι slide rules επιτρέπουν άλλους υπολογισμούς, όπως τετραγωνικές ρίζες, εκθετικά, λογαρίθμους και τριγωνομετρικές συναρτήσεις.

Οι μαθηματικοί υπολογισμοί γίνονται με την ευθυγράμμιση ενός σημείου στην ολισθαίνουσα κεντρική λωρίδα με ένα σημείο σε μία από τις σταθερές λωρίδες. Η σχετική θέση των άλλων σημάτων μπορεί στη συνέχεια να παρατηρηθεί. Οι αριθμοί που ευθυγραμμίζονται με τα σημάδια δίνουν την κατά προσέγγιση τιμή του γινομένου, του πηλίκου ή άλλου υπολογισμένου αποτελέσματος.

Ο χρήστης καθορίζει τη θέση του δεκαδικού σημείου στο αποτέλεσμα, με βάση τη νοητική εκτίμηση. Η επιστημονική σημειογραφία χρησιμοποιείται για την παρακολούθηση του δεκαδικού σημείου σε πιο επίσημους υπολογισμούς. Τα βήματα πρόσθεσης και αφαίρεσης σε έναν υπολογισμό γίνονται γενικά νοερά ή σε χαρτί, όχι στον κανόνα.

Οι περισσότεροι κανόνες διαφάνειας έχουν τρεις γραμμικές λωρίδες ίδιου μήκους. Οι λωρίδες είναι ευθυγραμμισμένες παράλληλα και αλληλοσυνδεόμενες έτσι ώστε η κεντρική λωρίδα να μπορεί να μετακινηθεί κατά μήκος σε σχέση με τις άλλες δύο. Οι δύο εξωτερικές λωρίδες είναι σταθερές έτσι ώστε η σχετική τους θέση να μην αλλάζει.

Ορισμένοι κανόνες διαφάνειας ("duplex" μοντέλα) έχουν κλίμακες και στις δύο πλευρές του κανόνα και της λωρίδας διαφάνειας, άλλοι στη μία πλευρά των εξωτερικών λωρίδων και στις δύο πλευρές της λωρίδας διαφάνειας, και άλλοι μόνο στη μία πλευρά ("simplex" κανόνες). Ένας δρομέας ολίσθησης με μια κάθετη γραμμή ευθυγράμμισης χρησιμοποιείται για την εύρεση αντίστοιχων σημείων σε κλίμακες που δεν βρίσκονται η μία δίπλα στην άλλη ή, στα μοντέλα duplex, βρίσκονται στην άλλη πλευρά του κανόνα. Ο δρομέας μπορεί επίσης να καταγράφει ένα ενδιάμεσο αποτέλεσμα σε οποιαδήποτε από τις κλίμακες.

Δρομέας σε slide rule

Χρήση κανόνα για τον υπολογισμό

Πολλαπλασιασμός

Ένας λογάριθμος μετατρέπει τις πράξεις του πολλαπλασιασμού και της διαίρεσης σε πρόσθεση και αφαίρεση σύμφωνα με τους κανόνες log ( x y ) = log ( x ) + log ( y ) {\displaystyle \log(xy)=\log(x)+\log(y)} και log ( x / y ) = log ( x ) - log ( y ) {\displaystyle \log(x/y)=\log(x)-\log(y)} . Μετακινώντας την επάνω κλίμακα προς τα δεξιά κατά μια απόσταση log ( x ) {\displaystyle \log(x)} , αντιστοιχίζοντας την αρχή της άνω κλίμακας με την ετικέτα x {\displaystyle x} στο κάτω μέρος, ευθυγραμμίζει κάθε αριθμό y {\displaystyle y} , στη θέση log ( y ) {\displaystyle \log(y)} στην επάνω κλίμακα, με τον αριθμό στη θέση log ( x ) + log ( y ) {\displaystyle \log(x)+\log(y)} στην κάτω κλίμακα. Επειδή log ( x ) + log ( y ) = log ( x y ) {\displaystyle \log(x)+\log(y)=\log(xy)} , αυτή η θέση στην κάτω κλίμακα δίνει x y {\displaystyle xy} , το γινόμενο των x {\displaystyle x} και y {\displaystyle y} . Για παράδειγμα, για τον υπολογισμό του 3*2, το 1 στην επάνω κλίμακα μετακινείται στο 2 στην κάτω κλίμακα. Η απάντηση, 6, διαβάζεται από την κάτω κλίμακα όπου το 3 βρίσκεται στην πάνω κλίμακα. Γενικά, το 1 στην επάνω κλίμακα μετακινείται σε έναν παράγοντα στην κάτω κλίμακα και η απάντηση διαβάζεται από την κάτω κλίμακα όπου ο άλλος παράγοντας βρίσκεται στην επάνω κλίμακα.

Για παράδειγμα, το παραπάνω διάγραμμα δείχνει ότι ο κανόνας δεν έχει τοποθετήσει το 7 στην πάνω κλίμακα πάνω από οποιονδήποτε αριθμό στην κάτω κλίμακα, οπότε δεν δίνει καμία απάντηση για το 2×7. Σε τέτοιες περιπτώσεις, ο χρήστης μπορεί να σύρει την επάνω κλίμακα προς τα αριστερά μέχρι ο δεξιός δείκτης της να ευθυγραμμιστεί με το 2, πολλαπλασιάζοντας ουσιαστικά με το 0,2 αντί με το 2, όπως στην παρακάτω εικόνα:

Εδώ ο χρήστης του κανόνα πρέπει να θυμάται να προσαρμόζει κατάλληλα το δεκαδικό σημείο για να διορθώσει την τελική απάντηση. Θέλαμε να βρούμε το 2×7, αλλά αντ' αυτού υπολογίσαμε 0,2×7=1,4. Έτσι, η πραγματική απάντηση δεν είναι 1,4 αλλά 14. Η επαναφορά της διαφάνειας δεν είναι ο μόνος τρόπος για να χειριστείτε πολλαπλασιασμούς που θα οδηγούσαν σε αποτελέσματα εκτός κλίμακας, όπως το 2×7- υπάρχουν και άλλες μέθοδοι:

• (1) Χρησιμοποιήστε τις κλίμακες διπλής δεκαετίας Α και Β.
• (2) Χρησιμοποιήστε τις διπλωμένες κλίμακες. Σε αυτό το παράδειγμα, ορίστε το αριστερό 1 του C απέναντι από το 2 του D. Μετακινήστε το δρομέα στο 7 στο CF και διαβάστε το αποτέλεσμα από το DF.
• (3) Χρησιμοποιήστε την ανεστραμμένη κλίμακα CI. Τοποθετήστε το 7 στην κλίμακα CI πάνω από το 2 στην κλίμακα D και, στη συνέχεια, διαβάστε το αποτέλεσμα στην κλίμακα D, κάτω από το 1 στην κλίμακα CI. Δεδομένου ότι το 1 εμφανίζεται σε δύο θέσεις στην κλίμακα CI, το ένα από αυτά θα είναι πάντα στην κλίμακα.
• (4) Χρησιμοποιήστε τόσο την ανεστραμμένη κλίμακα CI όσο και την κλίμακα C. Ευθυγραμμίστε το 2 του CI με το 1 του D και διαβάστε το αποτέλεσμα από το D, κάτω από το 7 της κλίμακας C.

Η μέθοδος 1 είναι εύκολα κατανοητή, αλλά συνεπάγεται απώλεια ακρίβειας. Η μέθοδος 3 έχει το πλεονέκτημα ότι περιλαμβάνει μόνο δύο κλίμακες.

Τμήμα

Η παρακάτω εικόνα δείχνει τον υπολογισμό του 5,5/2. Το 2 στην επάνω κλίμακα τοποθετείται πάνω από το 5,5 στην κάτω κλίμακα. Το 1 στην επάνω κλίμακα βρίσκεται πάνω από το πηλίκο, 2,75. Υπάρχουν περισσότερες από μία μέθοδοι για την εκτέλεση της διαίρεσης, αλλά η μέθοδος που παρουσιάζεται εδώ έχει το πλεονέκτημα ότι το τελικό αποτέλεσμα δεν μπορεί να είναι εκτός κλίμακας, επειδή έχει κανείς την επιλογή να χρησιμοποιήσει το 1 και στα δύο άκρα.

Άλλες εργασίες

Εκτός από τις λογαριθμικές κλίμακες, ορισμένοι διαβήτες διαθέτουν και άλλες μαθηματικές λειτουργίες κωδικοποιημένες σε άλλες βοηθητικές κλίμακες. Οι πιο δημοφιλείς ήταν οι τριγωνομετρικές, συνήθως ημίτονο και εφαπτομένη, κοινός λογάριθμος (log10) (για τη λήψη του λογαρίθμου μιας τιμής σε κλίμακα πολλαπλασιαστή), φυσικός λογάριθμος (ln) και εκθετική (e^x ) κλίμακα. Ορισμένοι κανόνες περιλαμβάνουν μια πυθαγόρεια κλίμακα, για να υπολογίσετε τις πλευρές τριγώνων, και μια κλίμακα για να υπολογίσετε κύκλους. Άλλοι διαθέτουν κλίμακες για τον υπολογισμό υπερβολικών συναρτήσεων. Στους γραμμικούς κανόνες, οι κλίμακες και η επισήμανσή τους είναι σε μεγάλο βαθμό τυποποιημένες, με διαφοροποιήσεις που συνήθως εμφανίζονται μόνο ως προς το ποιες κλίμακες περιλαμβάνονται και με ποια σειρά:

A, B	λογαριθμικές κλίμακες δύο δεκαετιών, που χρησιμοποιούνται για την εύρεση τετραγωνικών ριζών και τετραγώνων αριθμών
C, D	λογαριθμικές κλίμακες μιας δεκαετίας
K	λογαριθμική κλίμακα τριών δεκαετιών, που χρησιμοποιείται για την εύρεση κυβικών ριζών και κύβων αριθμών
CF, DF	"διπλωμένες" εκδόσεις των κλιμάκων C και D που ξεκινούν από το π και όχι από τη μονάδα- αυτές είναι βολικές σε δύο περιπτώσεις. Πρώτον, όταν ο χρήστης υποθέτει ότι ένα προϊόν θα είναι κοντά στο 10, αλλά δεν είναι σίγουρος αν θα είναι λίγο λιγότερο ή λίγο περισσότερο από το 10, οι διπλωμένες κλίμακες αποφεύγουν την πιθανότητα να ξεφύγει από την κλίμακα. Δεύτερον, κάνοντας την αρχή π αντί για την τετραγωνική ρίζα του 10, απλοποιείται ο πολλαπλασιασμός ή η διαίρεση με το π (όπως συνηθίζεται στους τύπους της επιστήμης και της μηχανικής).
CI, DI, DIF	"ανεστραμμένες" κλίμακες, από τα δεξιά προς τα αριστερά, που χρησιμοποιούνται για την απλούστευση των βημάτων 1/x
S	χρησιμοποιείται για την εύρεση ημιτόνων και συνημιτόνων στην κλίμακα D
T	χρησιμοποιείται για την εύρεση εφαπτόμενων και κοτογωνίων στις κλίμακες D και DI
ST, SRT	χρησιμοποιείται για ημιτόνια και εφαπτόμενες μικρών γωνιών και μετατροπή μοίρας-ακτίνας
L	μια γραμμική κλίμακα, που χρησιμοποιείται μαζί με τις κλίμακες C και D για την εύρεση λογαρίθμων της βάσης 10 και δυνάμεων του 10
LLn	ένα σύνολο κλιμάκων log-log, που χρησιμοποιούνται για την εύρεση λογαρίθμων και εκθετικών αριθμών
Ln	μια γραμμική κλίμακα, που χρησιμοποιείται μαζί με τις κλίμακες C και D για την εύρεση των φυσικών (βάση e) λογαρίθμων και e x {\displaystyle e^{x}}

 

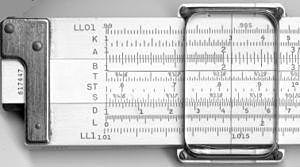
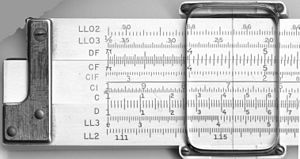
Οι κλίμακες στο μπροστινό και το πίσω μέρος ενός slide rule K&E 4081-3.

Ο δυαδικός συρόμενος κανόνας που κατασκευάστηκε από την Gilson το 1931 εκτελούσε μια λειτουργία πρόσθεσης και αφαίρεσης που περιοριζόταν στα κλάσματα.

Ρίζες και εξουσίες

Υπάρχουν κλίμακες μίας δεκαετίας (C και D), διπλής δεκαετίας (A και B) και τριπλής δεκαετίας (K). Για τον υπολογισμό του x 2 {\displaystyle x^{2}} , για παράδειγμα, εντοπίστε το x στην κλίμακα D και διαβάστε το τετράγωνό του στην κλίμακα A. Η αντιστροφή αυτής της διαδικασίας επιτρέπει την εύρεση τετραγωνικών ριζών και ομοίως για τις δυνάμεις 3, 1/3, 2/3 και 3/2. Πρέπει να δίνεται προσοχή όταν η βάση, x, βρίσκεται σε περισσότερα από ένα σημεία της κλίμακας της. Για παράδειγμα, υπάρχουν δύο εννιάρια στην κλίμακα Α- για να βρείτε την τετραγωνική ρίζα του εννιά, χρησιμοποιήστε το πρώτο- το δεύτερο δίνει την τετραγωνική ρίζα του 90.

Για προβλήματα x y {\displaystyle x^{y}}, χρησιμοποιήστε τις κλίμακες LL. Όταν υπάρχουν πολλές κλίμακες LL, χρησιμοποιήστε αυτή με το x. Αρχικά, ευθυγραμμίστε το πιο αριστερό 1 στην κλίμακα C με το x στην κλίμακα LL. Στη συνέχεια, βρείτε το y στην κλίμακα C και μεταβείτε στην κλίμακα LL με το x σε αυτήν. Αυτή η κλίμακα θα δείξει την απάντηση. Εάν το y είναι "εκτός κλίμακας", εντοπίστε το x y / 2 {\displaystyle x^{y/2}} και τετραγωνίστε το χρησιμοποιώντας τις κλίμακες Α και Β όπως περιγράφεται παραπάνω.

Τριγωνομετρία

Οι κλίμακες S, T και ST χρησιμοποιούνται για τριγωνομετρικές συναρτήσεις και πολλαπλάσια τριγωνομετρικών συναρτήσεων, για γωνίες σε μοίρες. Πολλοί slide rules έχουν τις κλίμακες S, T και ST με ενδείξεις σε μοίρες και λεπτά. Τα λεγόμενα μοντέλα decitrig χρησιμοποιούν αντ' αυτού δεκαδικά κλάσματα των μοιρών.

Λογάριθμοι και εκθετικά

Οι λογάριθμοι και οι εκθετικοί της βάσης 10 βρίσκονται χρησιμοποιώντας την κλίμακα L, η οποία είναι γραμμική. Ορισμένοι slide rules διαθέτουν κλίμακα Ln, η οποία είναι για τη βάση e.

Η κλίμακα Ln εφευρέθηκε από έναν μαθητή της 11ης τάξης, τον Stephen B. Cohen, το 1958. Η αρχική πρόθεση ήταν να επιτρέψει στο χρήστη να επιλέξει έναν εκθέτη x (στο εύρος 0 έως 2,3) στην κλίμακα Ln και να διαβάσει e^x στην κλίμακα C (ή D) και e^–x στην κλίμακα CI (ή DI). Η Pickett, Inc. απέκτησε τα αποκλειστικά δικαιώματα για την κλίμακα. Αργότερα, ο εφευρέτης δημιούργησε μια σειρά από "σημάδια" στην κλίμακα Ln για να επεκτείνει το εύρος πέρα από το όριο 2,3, αλλά η Pickett δεν ενσωμάτωσε ποτέ αυτά τα σημάδια σε κανέναν από τους συρόμενους κανόνες της. ^[]

Πρόσθεση και αφαίρεση

Οι κανόνες ολίσθησης δεν χρησιμοποιούνται συνήθως για πρόσθεση και αφαίρεση, αλλά είναι ωστόσο δυνατό να το κάνετε χρησιμοποιώντας δύο διαφορετικές τεχνικές.

Η πρώτη μέθοδος για την εκτέλεση της πρόσθεσης και της αφαίρεσης στις κλίμακες C και D (ή σε οποιαδήποτε συγκρίσιμη κλίμακα) απαιτεί τη μετατροπή του προβλήματος σε πρόβλημα διαίρεσης. Για την πρόσθεση, το πηλίκο των δύο μεταβλητών συν ένα επί τον διαιρέτη ισούται με το άθροισμά τους:

x + y = ( x y + 1 ) y {\displaystyle x+y=\left({\frac {x}{y}}+1\right)y}

Για την αφαίρεση, το πηλίκο των δύο μεταβλητών μείον ένα επί τον διαιρέτη ισούται με τη διαφορά τους:

x - y = ( x y - 1 ) y {\displaystyle x-y=\left({\frac {x}{y}}-1\right)y}

Η μέθοδος αυτή είναι παρόμοια με την τεχνική πρόσθεσης/αφαίρεσης που χρησιμοποιείται για ηλεκτρονικά κυκλώματα υψηλής ταχύτητας με το λογαριθμικό σύστημα αριθμών σε εξειδικευμένες εφαρμογές υπολογιστών όπως ο υπερυπολογιστής Gravity Pipe (GRAPE) και τα κρυφά μοντέλα Markov.

Η δεύτερη μέθοδος χρησιμοποιεί μια ολισθαίνουσα γραμμική κλίμακα L που διατίθεται σε ορισμένα μοντέλα. Η πρόσθεση και η αφαίρεση εκτελούνται με ολίσθηση του δρομέα προς τα αριστερά (για αφαίρεση) ή προς τα δεξιά (για πρόσθεση) και στη συνέχεια με επιστροφή της ολίσθησης στο 0 για ανάγνωση του αποτελέσματος.

Φυσικός σχεδιασμός

Τυπικοί γραμμικοί κανόνες

Το μήκος του αντικειμενοφόρου κανόνα αναφέρεται ως προς το ονομαστικό μήκος των κλιμάκων. Οι κλίμακες στα πιο συνηθισμένα μοντέλα "10 ιντσών" έχουν στην πραγματικότητα μήκος 25 cm, καθώς κατασκευάστηκαν σύμφωνα με τα μετρικά πρότυπα, αν και ορισμένοι κανόνες προσφέρουν ελαφρώς εκτεταμένες κλίμακες για την απλούστευση του χειρισμού όταν ένα αποτέλεσμα υπερχειλίζει. Οι κανόνες τσέπης είναι συνήθως 5 ίντσες. Μοντέλα μήκους μερικών μέτρων πωλούνταν για να κρεμαστούν σε αίθουσες διδασκαλίας για διδακτικούς σκοπούς. [1]

Συνήθως τα τμήματα σημειώνουν μια κλίμακα με ακρίβεια δύο σημαντικών ψηφίων και ο χρήστης εκτιμά το τρίτο ψηφίο. Ορισμένοι κανόνες διαφανειών υψηλών προδιαγραφών διαθέτουν μεγεθυντικούς δείκτες που κάνουν τις σημάνσεις πιο ευδιάκριτες. Τέτοιοι δείκτες μπορούν να διπλασιάσουν αποτελεσματικά την ακρίβεια των μετρήσεων, επιτρέποντας σε έναν κανόνα διαφάνειας 10 ιντσών να χρησιμεύσει εξίσου καλά με έναν 20 ιντσών.

Έχουν αναπτυχθεί διάφορες άλλες ευκολίες. Οι τριγωνομετρικές κλίμακες μερικές φορές φέρουν διπλή σήμανση, με μαύρο και κόκκινο χρώμα, με συμπληρωματικές γωνίες, το λεγόμενο στυλ "Darmstadt". Οι διπλοί κανόνες διαφάνειας συχνά αναπαράγουν ορισμένες από τις κλίμακες στο πίσω μέρος. Οι κλίμακες συχνά "χωρίζονται" για να επιτευχθεί μεγαλύτερη ακρίβεια.

Εξειδικευμένοι διαβήτες εφευρέθηκαν για διάφορες μορφές μηχανικής, επιχειρήσεων και τραπεζών. Αυτοί συχνά είχαν κοινούς υπολογισμούς που εκφράζονταν απευθείας ως ειδικές κλίμακες, για παράδειγμα υπολογισμούς δανείων, βέλτιστες ποσότητες αγοράς ή συγκεκριμένες εξισώσεις μηχανικής. Για παράδειγμα, η εταιρεία Fisher Controls διέθετε έναν προσαρμοσμένο διαφανειακό κανόνα προσαρμοσμένο στην επίλυση των εξισώσεων που χρησιμοποιούνταν για την επιλογή του κατάλληλου μεγέθους των βιομηχανικών βαλβίδων ελέγχου ροής. ^[]

Κυκλικοί κανόνες διαφάνειας

Οι κυκλικοί διαβήτες διατίθενται σε δύο βασικούς τύπους, ένας με δύο δρομείς (αριστερά) και ένας άλλος με κινητό δίσκο και έναν μόνο δρομέα (δεξιά). Οι εκδόσεις με δύο δρομείς εκτελούν πολλαπλασιασμό και διαίρεση διατηρώντας μια σταθερή γωνία μεταξύ των δρομέων καθώς περιστρέφονται γύρω από τον δίσκο. Η έκδοση με έναν μόνο δρομέα λειτουργεί περισσότερο σαν τον τυπικό slide rule μέσω της κατάλληλης ευθυγράμμισης των κλιμάκων.

Το βασικό πλεονέκτημα του κυκλικού κανόνα ολίσθησης είναι ότι η μεγαλύτερη διάσταση του εργαλείου μειώθηκε κατά έναν παράγοντα περίπου 3 (δηλαδή κατά π). Για παράδειγμα, η εξωτερική κλίμακα ενός κυκλικού κανόνα 10 cm θα είχε μέγιστη ακρίβεια ίση με έναν συνηθισμένο κανόνα 30 cm. Οι κυκλικοί ρυθμιστές διαφάνειας εξαλείφουν επίσης τους υπολογισμούς "εκτός κλίμακας", επειδή οι κλίμακες σχεδιάστηκαν για να "τυλίγονται γύρω-γύρω"- δεν χρειάζεται ποτέ να επαναπροσανατολιστούν όταν τα αποτελέσματα είναι κοντά στο 1,0 - ο κανόνας είναι πάντα στην κλίμακα. Ωστόσο, για τις μη κυκλικές μη σπειροειδείς κλίμακες, όπως οι κλίμακες S, T και LL, το μήκος της κλίμακας μειώνεται για να δημιουργηθεί χώρος για τα ακραία περιθώρια.

Οι κυκλικοί ρυθμιστές διαφάνειας είναι μηχανικά πιο ανθεκτικοί και πιο ομαλά κινούμενοι, αλλά η ακρίβεια ευθυγράμμισης της κλίμακας τους είναι ευαίσθητη στο κεντράρισμα ενός κεντρικού άξονα- ένα λεπτό 0,1 mm εκτός κέντρου του άξονα μπορεί να οδηγήσει σε σφάλμα ευθυγράμμισης 0,2 mm στη χειρότερη περίπτωση. Ο άξονας, ωστόσο, αποτρέπει το γρατσούνισμα της πρόσοψης και των δρομέων. Οι κλίμακες υψηλότερης ακρίβειας τοποθετούνται στους εξωτερικούς δακτυλίους. Αντί για "διαιρεμένες" κλίμακες, οι κυκλικοί κανόνες υψηλής ποιότητας χρησιμοποιούν σπειροειδείς κλίμακες για πιο σύνθετες λειτουργίες, όπως οι κλίμακες log-of-log. Ένας κυκλικός κανόνας υψηλής ποιότητας οκτώ ιντσών είχε μια σπειροειδή κλίμακα log-log 50 ιντσών.

Τα κύρια μειονεκτήματα των κυκλικών αντικειμενοφόρων είναι η δυσκολία εντοπισμού των αριθμών κατά μήκος ενός περιστρεφόμενου δίσκου και ο περιορισμένος αριθμός κλιμάκων. Ένα άλλο μειονέκτημα των κυκλικών αντικειμενοφόρων ράβδων είναι ότι οι λιγότερο σημαντικές κλίμακες βρίσκονται πιο κοντά στο κέντρο και έχουν μικρότερη ακρίβεια. Οι περισσότεροι μαθητές έμαθαν τη χρήση των αντικειμενοφόρων ράβδων με τους γραμμικούς αντικειμενοφόρους ράβδους και δεν βρήκαν λόγο να αλλάξουν.

Ένας κανόνας διαφάνειας που παραμένει σε καθημερινή χρήση σε όλο τον κόσμο είναι ο E6B. Πρόκειται για έναν κυκλικό slide rule που δημιουργήθηκε για πρώτη φορά τη δεκαετία του 1930 για τους πιλότους αεροσκαφών για να βοηθήσει στον υπολογισμό των νεκρών σημείων. Με τη βοήθεια των κλιμάκων που είναι τυπωμένες στο πλαίσιο βοηθά επίσης σε διάφορες εργασίες όπως η μετατροπή του χρόνου, της απόστασης, της ταχύτητας και των τιμών θερμοκρασίας, τα σφάλματα της πυξίδας και ο υπολογισμός της χρήσης καυσίμων. Ο λεγόμενος "τροχός προσευχής" είναι ακόμη διαθέσιμος σε καταστήματα αεροπορικών ειδών και εξακολουθεί να χρησιμοποιείται ευρέως. Ενώ το GPS έχει μειώσει τη χρήση του νεκρού υπολογισμού για την εναέρια πλοήγηση και οι υπολογιστές χειρός έχουν αναλάβει πολλές από τις λειτουργίες του, το E6B εξακολουθεί να χρησιμοποιείται ευρέως ως κύρια ή εφεδρική συσκευή και η πλειονότητα των σχολών πτήσης απαιτεί από τους μαθητές τους να κατέχουν σε κάποιο βαθμό τη χρήση του.

Το 1952, η ελβετική εταιρεία ρολογιών Breitling παρουσίασε ένα ρολόι χειρός πιλότου με ενσωματωμένο στρογγυλό slide rule, εξειδικευμένο για υπολογισμούς πτήσεων: το Breitling Navitimer. Ο κυκλικός κανόνας Navitimer, ο οποίος αναφερόταν από την Breitling ως "υπολογιστής πλοήγησης", διέθετε λειτουργίες ταχύτητας αέρα, ρυθμού/χρόνου ανόδου/καθόδου, χρόνου πτήσης, απόστασης και κατανάλωσης καυσίμου, καθώς και λειτουργίες μετατροπής χιλιομέτρων-ναυτικού μιλίου και ποσότητας καυσίμου σε γαλόνι-λίτρο.

Υλικά

Παραδοσιακά οι διαβήτες κατασκευάζονταν από σκληρό ξύλο, όπως το μαόνι ή το πυξάρι, με δρομείς από γυαλί και μέταλλο. Τουλάχιστον ένα όργανο υψηλής ακρίβειας ήταν κατασκευασμένο από χάλυβα.

Το 1895, μια ιαπωνική εταιρεία, η Hemmi, άρχισε να κατασκευάζει διαβήτες από μπαμπού, το οποίο είχε τα πλεονεκτήματα της σταθερότητας των διαστάσεων, της αντοχής και της φυσικής αυτολίπανσης. Αυτοί οι διαβήτες από μπαμπού παρουσιάστηκαν στη Σουηδία τον Σεπτέμβριο του 1933 [2], και πιθανώς λίγο νωρίτερα στη Γερμανία. Οι κλίμακες ήταν κατασκευασμένες από κυτταροειδές ή πλαστικό. Αργότερα οι διαβήτες κατασκευάστηκαν από πλαστικό ή από αλουμίνιο βαμμένο με πλαστικό. Οι μεταγενέστεροι δρομείς ήταν ακρυλικά ή πολυκαρβονικά που ολισθαίνουν σε ρουλεμάν από τεφλόν.

Σε όλους τους διαφανείς κανόνες υψηλής ποιότητας είχαν χαραχθεί αριθμοί και κλίμακες και στη συνέχεια είχαν γεμίσει με χρώμα ή άλλη ρητίνη. Οι βαμμένοι ή αποτυπωμένοι κανόνες θεωρούνταν κατώτεροι, επειδή οι σημάνσεις μπορούσαν να φθαρούν. Παρ' όλα αυτά, η Pickett, ίσως η πιο επιτυχημένη αμερικανική εταιρεία κανόνων διαφανειών, κατασκεύαζε όλες τις τυπωμένες κλίμακες. Οι premium slide rules περιλάμβαναν έξυπνες ασφάλειες ώστε ο κανόνας να μην διαλύεται κατά λάθος, καθώς και προφυλακτήρες για την προστασία των κλιμάκων και του δρομέα από την τριβή σε τραπέζια. Η συνιστώμενη μέθοδος καθαρισμού για τις χαραγμένες σημάνσεις είναι το ελαφρύ τρίψιμο με ατσαλόμαλλο μαλλί. Για τους ζωγραφισμένους κανόνες διαφανειών, και για τους λιπόψυχους, χρησιμοποιήστε αραιωμένο υγρό καθαρισμού παραθύρων του εμπορίου και ένα μαλακό πανί.

Κυκλικός κανόνας διαφάνειας Pickett με δύο δρομείς. (Διάμετρος 4,25 in./10,9 cm) Η πίσω όψη έχει πρόσθετη κλίμακα και έναν δρομέα.


Ένας απλός κυκλικός ρυθμιστικός κανόνας, κατασκευασμένος από την Concise Co., Ltd., Τόκιο, Ιαπωνία, με μόνο αντίστροφη, τετραγωνική και κυβική κλίμακα. Στο πίσω μέρος υπάρχει ένας εύχρηστος κατάλογος με 38 μετρικούς/αυτοκρατορικούς συντελεστές μετατροπής.


Ρολόι χειρός Breitling Navitimer με κυκλικό ρυθμιστικό κανόνα

Ιστορία

Ο slide rule εφευρέθηκε γύρω στα 1620-1630, λίγο μετά τη δημοσίευση της έννοιας του λογαρίθμου από τον John Napier. Ο Edmund Gunter από την Οξφόρδη ανέπτυξε μια υπολογιστική συσκευή με ενιαία λογαριθμική κλίμακα, η οποία, με πρόσθετα εργαλεία μέτρησης, μπορούσε να χρησιμοποιηθεί για πολλαπλασιασμό και διαίρεση. Η πρώτη περιγραφή αυτής της κλίμακας δημοσιεύθηκε στο Παρίσι το 1624 από τον Edmund Wingate (περ. 1593 - 1656), έναν Άγγλο μαθηματικό, σε ένα βιβλίο με τίτλο "L'usage de la reigle de proportion en l'arithmetique & geometrie". Το βιβλίο περιέχει μια διπλή κλίμακα στη μία πλευρά της οποίας υπάρχει μια λογαριθμική κλίμακα και στην άλλη μια πινακοποιημένη κλίμακα. Το 1630, ο William Oughtred από το Κέιμπριτζ εφηύρε έναν κυκλικό slide rule και το 1632 συνδύασε δύο κανόνες Gunter, που κρατιόντουσαν μαζί με τα χέρια, για να φτιάξει μια συσκευή που είναι αναγνωρίσιμα ο σύγχρονος slide rule. Όπως και ο σύγχρονος του στο Κέιμπριτζ, Ισαάκ Νεύτων, ο Όουτρεντ δίδαξε τις ιδέες του κατ' ιδίαν στους μαθητές του, αλλά καθυστέρησε να τις δημοσιεύσει, και όπως ο Νεύτων, ενεπλάκη σε μια βιτριολική διαμάχη για την προτεραιότητα, με τον πρώην μαθητή του Ρίτσαρντ Ντελαμέιν και τις προηγούμενες αξιώσεις του Γουίνγκεϊτ. Οι ιδέες του Όουτρεντ δημοσιοποιήθηκαν μόνο σε δημοσιεύσεις του μαθητή του Γουίλιαμ Φόρστερ το 1632 και το 1653.

Το 1677, ο Henry Coggeshall δημιούργησε έναν πτυσσόμενο κανόνα δύο ποδιών για τη μέτρηση της ξυλείας, ο οποίος ονομάστηκε Coggeshall slide rule. Ο σχεδιασμός του και οι χρήσεις του εργαλείου του έδωσαν στον διαβήτη σκοπό εκτός της μαθηματικής έρευνας.

Το 1722, ο Warner εισήγαγε τις κλίμακες δύο και τριών δεκαετιών, και το 1755 ο Everard συμπεριέλαβε μια ανεστραμμένη κλίμακα.Ένας κανόνας που περιέχει όλες αυτές τις κλίμακες είναι συνήθως γνωστός ως "πολυφασικός" κανόνας.

Το 1815, ο Peter Roget εφηύρε τον λογαριθμικό κανόνα, ο οποίος περιλάμβανε μια κλίμακα που εμφάνιζε τον λογάριθμο του λογαρίθμου. Αυτό επέτρεπε στον χρήστη να εκτελεί άμεσα υπολογισμούς που αφορούσαν ρίζες και εκθέτες. Αυτό ήταν ιδιαίτερα χρήσιμο για τις κλασματικές δυνάμεις.

Σύγχρονη μορφή

Η πιο σύγχρονη μορφή δημιουργήθηκε το 1859 από τον Γάλλο υπολοχαγό πυροβολικού Amédée Mannheim, "ο οποίος είχε την τύχη να κατασκευάσει τον κανόνα του από μια εταιρεία εθνικής φήμης και να τον υιοθετήσει το Γαλλικό Πυροβολικό". Περίπου εκείνη την εποχή, καθώς η μηχανική έγινε αναγνωρισμένη επαγγελματική δραστηριότητα, οι συρόμενοι κανόνες άρχισαν να χρησιμοποιούνται ευρέως στην Ευρώπη. Δεν έγιναν κοινοί στις Ηνωμένες Πολιτείες μέχρι το 1881, όταν ο Edwin Thacher εισήγαγε εκεί έναν κυλινδρικό κανόνα. Ο διπλός κανόνας εφευρέθηκε από τον William Cox το 1891 και κατασκευάστηκε από την Keuffel and Esser Co. της Νέας Υόρκης.

Οι αστρονομικές εργασίες απαιτούσαν επίσης λεπτούς υπολογισμούς, και στη Γερμανία του 19ου αιώνα σε ένα αστεροσκοπείο χρησιμοποιούνταν ένας ατσάλινος διαφανής κανόνας μήκους περίπου 2 μέτρων. Είχε προσαρτημένο ένα μικροσκόπιο, που του έδινε ακρίβεια έξι δεκαδικών ψηφίων.

Στον Β' Παγκόσμιο Πόλεμο, οι βομβαρδιστές και οι πλοηγοί που χρειάζονταν γρήγορους υπολογισμούς χρησιμοποιούσαν συχνά εξειδικευμένους διαφανείς κανόνες. Ένα γραφείο του Πολεμικού Ναυτικού των ΗΠΑ σχεδίασε στην πραγματικότητα ένα γενικό "πλαίσιο" με αλουμινένιο σώμα και πλαστικό δρομέα, στο οποίο μπορούσαν να τοποθετηθούν κάρτες από κυτταροειδές (τυπωμένες και στις δύο όψεις) για ειδικούς υπολογισμούς. Η διαδικασία εφευρέθηκε για τον υπολογισμό της εμβέλειας, της χρήσης καυσίμων και του ύψους για αεροσκάφη και στη συνέχεια προσαρμόστηκε σε πολλούς άλλους σκοπούς.

Σε όλη τη δεκαετία του 1950 και του 1960 ο κανόνας διαφάνειας ήταν το σύμβολο του επαγγέλματος του μηχανικού (με τον ίδιο τρόπο που το στηθοσκόπιο συμβολίζει το ιατρικό επάγγελμα).^[] Ο Γερμανός επιστήμονας πυραύλων Wernher von Braun έφερε μαζί του δύο slide rules της δεκαετίας του 1930 της Nestler, όταν μετακόμισε στις ΗΠΑ μετά τον Β' Παγκόσμιο Πόλεμο για να εργαστεί στο αμερικανικό διαστημικό πρόγραμμα. Καθ' όλη τη διάρκεια της ζωής του δεν χρησιμοποίησε ποτέ άλλες υπολογιστικές συσκευές τσέπης- οι διαφανείς κανόνες του χρησίμευαν άριστα για να κάνει γρήγορες εκτιμήσεις των παραμέτρων σχεδιασμού πυραύλων και άλλων αριθμών. Οι αλουμινένιοι διαβήτες μάρκας Pickett μεταφέρθηκαν σε πέντε διαστημικές αποστολές Apollo, μεταξύ των οποίων και στο φεγγάρι, σύμφωνα με τη διαφήμιση στα κουτιά με τους διαβήτες N600 της Pickett [3].

Ορισμένοι φοιτητές μηχανικοί και μηχανικοί μετέφεραν σε θήκες ζώνης διαφανειών δέκα ιντσών, και ακόμη και στα μέσα της δεκαετίας του 1970 αυτό ήταν συνηθισμένο θέαμα στις πανεπιστημιουπόλεις. Οι φοιτητές μπορεί επίσης να κρατούσαν έναν κανόνα δέκα ή είκοσι ιντσών για εργασίες ακριβείας στο σπίτι ή στο γραφείο, ενώ κουβαλούσαν μαζί τους έναν κανόνα πέντε ιντσών τσέπης.

Το 2004, οι ερευνητές της εκπαίδευσης David B. Sher και Dean C. Nataro σχεδίασαν έναν νέο τύπο κανόνα διαφάνειας που βασίζεται στην προσταφαίρεση, έναν αλγόριθμο για τον γρήγορο υπολογισμό προϊόντων που προϋπήρχε των λογαρίθμων. Ωστόσο, υπήρξε μικρό πρακτικό ενδιαφέρον για την κατασκευή ενός τέτοιου, πέρα από το αρχικό πρωτότυπο. [4]

Πτώση

Η σημασία του διαβήτη άρχισε να μειώνεται καθώς οι ηλεκτρονικοί υπολογιστές, ένας νέος αλλά πολύ σπάνιος πόρος στη δεκαετία του 1950, έγιναν ευρέως διαθέσιμοι στους τεχνικούς εργαζόμενους κατά τη δεκαετία του 1960. Η εισαγωγή της Fortran το 1957 κατέστησε τους υπολογιστές πρακτικούς για την επίλυση μαθηματικών προβλημάτων μικρού μεγέθους. Η IBM εισήγαγε μια σειρά πιο προσιτών υπολογιστών, τους IBM 650 (1954), IBM 1620 (1959), IBM 1130 (1965) που απευθύνονταν στην αγορά των επιστημόνων και των μηχανικών. Η γλώσσα προγραμματισμού BASIC του John Kemeny (1964) έκανε εύκολη τη χρήση των υπολογιστών από τους φοιτητές. Ο μίνι υπολογιστής DEC PDP-8 παρουσιάστηκε το 1965.

Οι υπολογιστές άλλαξαν επίσης τη φύση των υπολογισμών. Με τους κανόνες διαφανειών, δόθηκε μεγάλη έμφαση στην επεξεργασία της άλγεβρας για να μετατραπούν οι εκφράσεις στην πιο υπολογίσιμη μορφή. Οι χρήστες των διαφανειών απλά προσέγγιζαν ή άφηναν μικρούς όρους για να απλοποιήσουν τον υπολογισμό. Η Fortran επέτρεψε την πληκτρολόγηση πολύπλοκων τύπων από εγχειρίδια χωρίς την προσπάθεια επαναδιατύπωσης. Η αριθμητική ολοκλήρωση ήταν συχνά ευκολότερη από την προσπάθεια εύρεσης λύσεων κλειστής μορφής για δύσκολα προβλήματα. Ο νεαρός μηχανικός που ζητούσε χρόνο από τον υπολογιστή για να λύσει ένα πρόβλημα που θα μπορούσε να είχε γίνει με μερικές κινήσεις στον κανόνα διαφανειών έγινε χιουμοριστικό κλισέ. Πολλά κέντρα υπολογιστών είχαν κρεμασμένο στον τοίχο έναν κορνιζαρισμένο κανόνα με τη σημείωση "Σε περίπτωση έκτακτης ανάγκης, σπάστε το γυαλί".

Ένα άλλο βήμα προς την αντικατάσταση των διαφανειών με ηλεκτρονικά μέσα ήταν η ανάπτυξη ηλεκτρονικών αριθμομηχανών για επιστημονική και μηχανολογική χρήση. Οι πρώτες περιελάμβαναν το Wang Laboratories LOCI-2, που παρουσιάστηκε το 1965, το οποίο χρησιμοποιούσε λογαρίθμους για πολλαπλασιασμό και διαίρεση και το Hewlett-Packard HP-9100, που παρουσιάστηκε το 1968. Η HP-9100 διέθετε τριγωνομετρικές συναρτήσεις (sin, cos, tan) εκτός από τα εκθετικά και τους λογαρίθμους. Χρησιμοποιούσε τον αλγόριθμο CORDIC (coordinate rotation digital computer), ο οποίος επιτρέπει τον υπολογισμό τριγωνομετρικών συναρτήσεων χρησιμοποιώντας μόνο πράξεις μετατόπισης και πρόσθεσης. Η μέθοδος αυτή διευκόλυνε την ανάπτυξη ολοένα και μικρότερων επιστημονικών αριθμομηχανών.

Το τελευταίο καρφί στο φέρετρο του κανόνα διαφανειών ήταν το λανσάρισμα των επιστημονικών αριθμομηχανών τσέπης, από τις οποίες η Hewlett-Packard HP-35 το 1972 ήταν η πρώτη. Τέτοιες αριθμομηχανές έγιναν γνωστές ως αριθμομηχανές με "κανόνα διαφάνειας", καθώς μπορούσαν να εκτελέσουν τις περισσότερες ή όλες τις λειτουργίες ενός κανόνα διαφάνειας. Με τιμή αρκετών εκατοντάδων δολαρίων, ακόμη και αυτή θεωρούνταν ακριβή για τους περισσότερους φοιτητές. Ενώ οι επαγγελματικοί υπολογιστές με διαφάνειες μπορούσαν επίσης να είναι αρκετά ακριβοί, τα φαρμακεία συχνά πωλούσαν βασικά πλαστικά μοντέλα για λιγότερο από 20 δολάρια ΗΠΑ. Αλλά μέχρι το 1975, οι βασικές ηλεκτρονικές αριθμομηχανές τεσσάρων λειτουργιών μπορούσαν να αγοραστούν για λιγότερο από 50 δολάρια. Μέχρι το 1976 το TI-30 προσέφερε μια επιστημονική αριθμομηχανή για λιγότερο από 25 δολάρια. Μετά από αυτό το διάστημα, η αγορά των κανόνων διαφάνειας στέρεψε γρήγορα, καθώς οι μικρές επιστημονικές αριθμομηχανές έγιναν προσιτές.

William Oughtred (1575-1660), εφευρέτης του κυκλικού κανόνα διαφάνειας


Μηχανικός που χρησιμοποιεί slide rule. Σημειώστε μηχανική αριθμομηχανή στο φόντο.


TI-30

Πλεονεκτήματα

• Ένας κανόνας τείνει να μετριάσει την πλάνη της "ψευδούς ακρίβειας" και της σημασίας. Η τυπική ακρίβεια που έχει στη διάθεσή του ο χρήστης ενός slide rule είναι περίπου τρεις θέσεις ακρίβειας. Αυτό βρίσκεται σε καλή αντιστοιχία με τα περισσότερα δεδομένα που είναι διαθέσιμα για την εισαγωγή σε τύπους μηχανικής. Όταν χρησιμοποιείται μια σύγχρονη αριθμομηχανή τσέπης, η ακρίβεια μπορεί να εμφανίζεται σε επτά ή περισσότερα δεκαδικά ψηφία, ενώ στην πραγματικότητα τα αποτελέσματα δεν μπορούν ποτέ να έχουν μεγαλύτερη ακρίβεια από τα διαθέσιμα δεδομένα εισόδου.
• Ο κανόνας διαφάνειας απαιτεί συνεχή εκτίμηση της τάξης μεγέθους των αποτελεσμάτων. Σε έναν slide rule το 1,5 × 30 (που ισούται με 45) θα δείξει το ίδιο αποτέλεσμα με το 1.500.000 × 0,03 (που ισούται με 45.000). Εναπόκειται στον μηχανικό να προσδιορίζει συνεχώς το εύλογο των αποτελεσμάτων, κάτι που μπορεί να χαθεί όταν οι αριθμοί εισάγονται απρόσεκτα σε ένα πρόγραμμα υπολογιστή ή σε μια αριθμομηχανή.
• Όταν εκτελείτε μια ακολουθία πολλαπλασιασμών ή διαιρέσεων με τον ίδιο αριθμό, η απάντηση μπορεί συχνά να προσδιοριστεί με μια απλή ματιά στον κανόνα χωρίς κανένα χειρισμό. Αυτό μπορεί να είναι ιδιαίτερα χρήσιμο κατά τον υπολογισμό ποσοστών, π.χ. για βαθμολογίες σε τεστ, ή κατά τη σύγκριση τιμών, π.χ. σε δολάρια ανά χιλιόγραμμο. Πολλαπλοί υπολογισμοί ταχύτητας-χρόνου-απόστασης μπορούν να εκτελεστούν χωρίς χέρια με μια ματιά με έναν κανόνα διαφάνειας.
• Ο κανόνας διαφάνειας δεν εξαρτάται από την ηλεκτρική ενέργεια.
• Ο φωτογραφικός κανόνας είναι μια τεχνολογία που αναπαράγεται εύκολα. Από ένα δεδομένο παράδειγμα κανόνα, μπορεί να κατασκευαστούν περισσότεροι από έναν ικανό τεχνίτη από υποτυπώδη υλικά με μη βιομηχανικές διαδικασίες.
• Οι κανόνες διαφανειών είναι σε μεγάλο βαθμό τυποποιημένοι, οπότε δεν χρειάζεται να ξαναμαθαίνετε τίποτα όταν αλλάζετε σε διαφορετικό κανόνα.
• Οι συρόμενοι κανόνες είναι ευέλικτοι και μπορούν να χρησιμοποιηθούν σε καταστάσεις και περιβάλλοντα όπου ο ανθρώπινος χρήστης μπορεί να έχει μειωμένη επιδεξιότητα (για παράδειγμα, λόγω της ανάγκης χρήσης προστατευτικών γαντιών). Αντίθετα, μια αριθμομηχανή μπορεί να είναι δύσκολο να λειτουργήσει σε τέτοιες καταστάσεις - ένας slide rule είναι απίθανο να οδηγήσει σε σφάλμα παρόμοιο με αυτό που προκύπτει από το λανθασμένο πάτημα του λάθος κουμπιού σε μια αριθμομηχανή.
• Οι συρόμενοι κανόνες μπορούν να κατασκευαστούν από χαρτόνι ή χαρτί. Πολλοί ελεύθεροι χάρτες ή εξειδικευμένες υπολογιστικές συσκευές από χαρτόνι είναι στην πραγματικότητα εξειδικευμένοι γραμμικοί ή κυκλικοί κανόνες διαφάνειας.

Ένα πλεονέκτημα της χρήσης ενός κανόνα με διαφάνεια μαζί με μια ηλεκτρονική αριθμομηχανή είναι ότι ένας σημαντικός υπολογισμός μπορεί να ελεγχθεί κάνοντάς τον και με τα δύο όργανα- επειδή τα δύο όργανα είναι τόσο διαφορετικά, υπάρχει μικρή πιθανότητα να γίνει το ίδιο λάθος δύο φορές.

Μειονεκτήματα

• Τα σφάλματα μπορεί να οφείλονται σε μηχανική ανακρίβεια.
• Οι υπολογισμοί με τη χρήση του κανόνα διαφάνειας είναι περιορισμένης ακρίβειας λόγω των αναλογικών εισόδων και εξόδων τους. Αντίθετα, λόγω των διακριτών αριθμητικών εισόδων και των ηλεκτρονικών λειτουργιών κινητής υποδιαστολής, ακόμη και οι μέτριες σύγχρονες αριθμομηχανές έχουν ανάλυση εξόδου τουλάχιστον έξι σημαντικών ψηφίων.

Σχετικές σελίδες

• Abacus
• Λογάριθμος