Γινόμενο τελείας

Ορισμός

Το τετραγωνικό γινόμενο δύο διανυσμάτων a = [a₁ , a₂ , ..., a_n ] και b = [b₁ , b₂ , ..., b_n ] ορίζεται ως εξής:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}}

όπου Σ συμβολίζει τον αθροιστικό συμβολισμό ( το άθροισμα όλων των όρων) και n είναι η διάσταση του διανυσματικού χώρου.

Στη διάσταση 2, το τετραγωνικό γινόμενο των διανυσμάτων [a,b] και [c,d] είναι ac + bd. Με τον ίδιο τρόπο, στη διάσταση 3, το τετραγωνικό γινόμενο των διανυσμάτων [a,b,c] και [d,e,f] είναι ad + be + cf. Για παράδειγμα, το τετραγωνικό γινόμενο δύο τρισδιάστατων διανυσμάτων [1, 3, -5] και [4, -2, -1] είναι

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.}

Γεωμετρική ερμηνεία

Στην ευκλείδεια γεωμετρία, το γινόμενο κουκκίδων, το μήκος και η γωνία σχετίζονται μεταξύ τους. Για ένα διάνυσμα a, το τετραγωνικό γινόμενο a - a είναι το τετράγωνο του μήκους του a, ή

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\left\|\mathbf {a} \right\|^{2}}

όπου ||a|| συμβολίζει το μήκος (μέγεθος) του a. Γενικότερα, αν το b είναι ένα άλλο διάνυσμα

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|cos \theta \,}

όπου ||a|| και ||b|| συμβολίζουν το μήκος των a και b και θ είναι η γωνία μεταξύ τους.

Ο τύπος αυτός μπορεί να αναδιαταχθεί για να προσδιοριστεί το μέγεθος της γωνίας μεταξύ δύο μη μηδενικών διανυσμάτων:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {\mathbf {a}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)}

Μπορούμε επίσης πρώτα να μετατρέψουμε τα διανύσματα σε μοναδιαία διανύσματα διαιρώντας τα με το μέγεθός τους:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}}

τότε η γωνία θ δίνεται από τη σχέση

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}\cdot {\boldsymbol {\hat {b}})}

Καθώς το συνημίτονο των 90° είναι μηδέν, το τετραγωνικό γινόμενο δύο ορθογώνιων (κάθετων) διανυσμάτων είναι πάντα μηδέν. Επιπλέον, δύο διανύσματα μπορούν να θεωρηθούν ορθογώνια εάν και μόνο εάν το τετραγωνικό τους γινόμενο είναι μηδέν και έχουν και τα δύο μη μηδενικό μήκος. Αυτή η ιδιότητα παρέχει μια απλή μέθοδο για τον έλεγχο της συνθήκης της ορθογωνιότητας.

Μερικές φορές αυτές οι ιδιότητες χρησιμοποιούνται επίσης για τον ορισμό του γινομένου κουκκίδων, ειδικά σε 2 και 3 διαστάσεις- ο ορισμός αυτός είναι ισοδύναμος με τον παραπάνω. Για μεγαλύτερες διαστάσεις ο τύπος μπορεί να χρησιμοποιηθεί για τον ορισμό της έννοιας της γωνίας.

Οι γεωμετρικές ιδιότητες βασίζονται στο ότι η βάση είναι ορθοκανονική, δηλαδή αποτελείται από κάθετα διανύσματα ανά ζεύγη με μοναδιαίο μήκος.

Κλιμακωτή προβολή

Εάν και τα δύο a και b έχουν μήκος ένα (δηλαδή είναι μοναδιαία διανύσματα), το γινόμενο τελείας τους δίνει απλώς το συνημίτονο της μεταξύ τους γωνίας.

Αν μόνο το b είναι μοναδιαίο διάνυσμα, τότε το γινόμενο τελείας a - b δίνει το |a| cos(θ), δηλαδή το μέγεθος της προβολής του a στην κατεύθυνση του b, με μείον πρόσημο αν η κατεύθυνση είναι αντίθετη. Αυτό ονομάζεται κλιμακωτή προβολή του a στο b, ή κλιμακωτή συνιστώσα του a στην κατεύθυνση του b (βλέπε σχήμα). Αυτή η ιδιότητα του τετραγωνικού γινομένου έχει πολλές χρήσιμες εφαρμογές (για παράδειγμα, βλ. επόμενη ενότητα).

Εάν ούτε το a ούτε το b είναι μοναδιαίο διάνυσμα, τότε το μέγεθος της προβολής του a στην κατεύθυνση του b, για παράδειγμα, θα είναι a - (b / |b|), καθώς το μοναδιαίο διάνυσμα στην κατεύθυνση του b είναι b / |b|.

Περιστροφή

Μια περιστροφή της ορθοκανονικής βάσης με βάση την οποία αναπαρίσταται το διάνυσμα a προκύπτει με πολλαπλασιασμό του a με έναν πίνακα περιστροφής R. Αυτός ο πολλαπλασιασμός του πίνακα είναι απλώς μια συμπαγής αναπαράσταση μιας ακολουθίας παραγώγων τελείας.

Για παράδειγμα, έστω

• B₁ = {x, y, z} και B₂ = {u, v, w} είναι δύο διαφορετικές ορθοκανονικές βάσεις του ίδιου χώρου R³ , με το B₂ να προκύπτει με απλή περιστροφή του B₁ ,
• a₁ = (a_x , a_y , a_z ) αντιπροσωπεύουν το διάνυσμα a ως προς το B ,₁
• a₂ = (a_u , a_v , a_w ) αντιπροσωπεύουν το ίδιο διάνυσμα ως προς την περιστρεφόμενη βάση B ,₂
• u₁ , v₁ , w₁ είναι τα διανύσματα u, v, w που αναπαρίστανται ως προς το B .₁

Στη συνέχεια, η περιστροφή από το B₁ στο B₂ πραγματοποιείται ως εξής:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}\{\{\mathbf {w}}_{1}\cdot {\mathbf {a}}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}\\a_{v}\\a_{w}\end{bmatrix}}. }

Σημειώστε ότι ο πίνακας περιστροφής R συναρμολογείται χρησιμοποιώντας τα διανύσματα περιστροφής u₁ , v₁ , w₁ ως γραμμές του και τα διανύσματα αυτά είναι μοναδιαία διανύσματα. Εξ ορισμού, ο Ra₁ αποτελείται από μια ακολουθία παραγώγων τελείας μεταξύ καθεμιάς από τις τρεις γραμμές του R και του διανύσματος a₁ . Κάθε ένα από αυτά τα γινόμενα τελείας καθορίζει μια κλιμακωτή συνιστώσα του a στην κατεύθυνση ενός διανύσματος περιστρεφόμενης βάσης (βλέπε προηγούμενη ενότητα).

Εάν ένα₁ είναι διάνυσμα γραμμής και όχι στήλης, τότε το R πρέπει να περιέχει τα διανύσματα της περιστρεφόμενης βάσης στις στήλες του και πρέπει να μεταπολλαπλασιάζει ένα₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

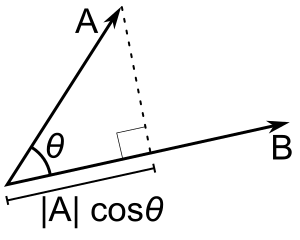
A - B = |A| |B| cos(θ). |A| cos(θ) είναι η κλιμακωτή προβολή του A στο B.

Φυσική

Στη φυσική, το μέγεθος είναι ένα κλιμάκιο με τη φυσική έννοια, δηλαδή ένα φυσικό μέγεθος ανεξάρτητο από το σύστημα συντεταγμένων, που εκφράζεται ως το γινόμενο μιας αριθμητικής τιμής και μιας φυσικής μονάδας, όχι απλώς ένας αριθμός. Το τετραγωνικό γινόμενο είναι επίσης ένα κλιμάκιο με αυτή την έννοια, που δίνεται από τον τύπο, ανεξάρτητο από το σύστημα συντεταγμένων. Παράδειγμα:

• Το μηχανικό έργο είναι το τετραγωνικό γινόμενο των διανυσμάτων δύναμης και μετατόπισης.
• Η μαγνητική ροή είναι το τετραγωνικό γινόμενο του μαγνητικού πεδίου και των διανυσμάτων περιοχής.
• Η ογκομετρική ροή είναι το τετραγωνικό γινόμενο της ταχύτητας του ρευστού και των διανυσμάτων εμβαδού.

Ιδιότητες

Οι ακόλουθες ιδιότητες ισχύουν εάν τα a, b και c είναι πραγματικά διανύσματα και το r είναι ένα κλιμάκιο.

Το γινόμενο τελείας είναι αντιμεταθετικό:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . }

Το τετραγωνικό γινόμενο είναι διανεμητικό επί της διανυσματικής πρόσθεσης:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . }

Το γινόμενο τελείας είναι διγραμμικό:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). }

Όταν πολλαπλασιάζεται με μια κλιμακωτή τιμή, το γινόμενο τελείας ικανοποιεί:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}

(οι δύο τελευταίες ιδιότητες προκύπτουν από τις δύο πρώτες).

Δύο μη μηδενικά διανύσματα a και b είναι κάθετα αν και μόνο αν a - b = 0.

Σε αντίθεση με τον πολλαπλασιασμό των συνηθισμένων αριθμών, όπου αν ab = ac, τότε το b ισούται πάντα με το c εκτός αν το a είναι μηδέν, το γινόμενο τελείας δεν υπακούει στο νόμο ακύρωσης:

Αν a - b = a - c και a ≠ 0, τότε μπορούμε να γράψουμε: a - (b - c) = 0 από τον διανεμητικό νόμο- το παραπάνω αποτέλεσμα λέει ότι αυτό απλά σημαίνει ότι το a είναι κάθετο στο (b - c), το οποίο εξακολουθεί να επιτρέπει (b - c) ≠ 0, και επομένως b ≠ c.

Με την προϋπόθεση ότι η βάση είναι ορθοκανονική, το γινόμενο κουκκίδων είναι αναλλοίωτο σε ισομετρικές αλλαγές της βάσης: περιστροφές, ανακλάσεις και συνδυασμούς, διατηρώντας την αρχή σταθερή. Η προαναφερθείσα γεωμετρική ερμηνεία βασίζεται σε αυτή την ιδιότητα. Με άλλα λόγια, για έναν ορθοκανονικό χώρο με οποιονδήποτε αριθμό διαστάσεων, το γινόμενο κουκκίδων είναι αναλλοίωτο κάτω από έναν μετασχηματισμό συντεταγμένων με βάση έναν ορθογώνιο πίνακα. Αυτό αντιστοιχεί στις ακόλουθες δύο συνθήκες:

• Η νέα βάση είναι και πάλι ορθοκανονική (δηλ. είναι ορθοκανονική εκφρασμένη στην παλιά βάση).
• Τα νέα διανύσματα βάσης έχουν το ίδιο μήκος με τα παλαιά (δηλ. μοναδιαίο μήκος ως προς την παλαιά βάση).

Αν τα a και b είναι συναρτήσεις, τότε η παράγωγος του a - b είναι a' - b + a - b'

Επέκταση τριπλού προϊόντος

Πρόκειται για μια πολύ χρήσιμη ταυτότητα (γνωστή και ως τύπος του Λαγκράνζ) που περιλαμβάνει τα τετραγωνικά και διασταυρούμενα γινόμενα. Γράφεται ως

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

το οποίο είναι ευκολότερο να το θυμάστε ως "BAC μείον CAB", έχοντας κατά νου ποια διανύσματα είναι διακεκομμένα μεταξύ τους. Αυτός ο τύπος χρησιμοποιείται συνήθως για την απλοποίηση των διανυσματικών υπολογισμών στη φυσική.

Απόδειξη της γεωμετρικής ερμηνείας

Εξετάστε το στοιχείο του R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + . . . . + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

Επαναλαμβανόμενη εφαρμογή του Πυθαγόρειου θεωρήματος δίνει για το μήκος του |v|

| v | 2 = v 1 2 + v 2 2 + . . . . + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Αλλά αυτό είναι το ίδιο με

v ⋅ v = v 1 2 + v 2 2 + . . . . + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

οπότε συμπεραίνουμε ότι το τετραγωνικό γινόμενο ενός διανύσματος v με τον εαυτό του δίνει το τετραγωνικό μήκος του διανύσματος.

Λήμμα 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Θεωρήστε τώρα δύο διανύσματα a και b που εκτείνονται από την αρχή και χωρίζονται από γωνία θ. Ένα τρίτο διάνυσμα c μπορεί να οριστεί ως εξής

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\ \mathbf {a} -\mathbf {b} .\,}

δημιουργώντας ένα τρίγωνο με πλευρές a, b και c. Σύμφωνα με το νόμο των συνημίτονων, έχουμε

| c | 2 = | a | 2 + | b | 2 - 2 | a | | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} |||\mathbf {b} |\cos \theta .\,}

Αντικαθιστώντας τα τετραγωνικά μήκη με γινόμενο κουκκίδων σύμφωνα με το Λήμμα 1, έχουμε

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} (1)

Αλλά καθώς c ≡ a - b, έχουμε επίσης

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} ,

η οποία, σύμφωνα με τον νόμο της διανομής, επεκτείνεται σε

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} (2)

Συγχωνεύοντας τις δύο c - c εξισώσεις, (1) και (2), λαμβάνουμε

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Η αφαίρεση του a - a + b - b και από τις δύο πλευρές και η διαίρεση με το -2 αφήνει

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} |||\mathbf {b} |\cos \theta .\,}

Q.E.D.

Γενίκευση

Το εσωτερικό γινόμενο γενικεύει το τετραγωνικό γινόμενο σε αφηρημένους διανυσματικούς χώρους και συνήθως συμβολίζεται ως εξής: ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } . Λόγω της γεωμετρικής ερμηνείας του τετραγωνικού γινομένου η νόρμα ||a|| ενός διανύσματος a σε έναν τέτοιο χώρο εσωτερικού γινομένου ορίζεται ως εξής

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

έτσι ώστε να γενικεύει το μήκος, και η γωνία θ μεταξύ δύο διανυσμάτων a και b με

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ ‖ b ‖ . {\displaystyle \cos \theta }={\frac \langle \mathbf {a} \,,\mathbf {b} \ \angle }{\|\mathbf {a} \|\,\|\\mathbf {b} \|}}. }

Ειδικότερα, δύο διανύσματα θεωρούνται ορθογώνια εάν το εσωτερικό τους γινόμενο είναι μηδέν.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \angle =0.}

Για διανύσματα με σύνθετες καταχωρήσεις, η χρήση του συγκεκριμένου ορισμού του τετραγωνικού γινομένου θα οδηγούσε σε αρκετά διαφορετικές γεωμετρικές ιδιότητες. Για παράδειγμα, το γινόμενο τελείας ενός διανύσματος με τον εαυτό του μπορεί να είναι ένας αυθαίρετος μιγαδικός αριθμός και μπορεί να είναι μηδέν χωρίς το διάνυσμα να είναι το μηδενικό διάνυσμα- αυτό με τη σειρά του θα είχε σοβαρές συνέπειες για έννοιες όπως το μήκος και η γωνία. Πολλές γεωμετρικές ιδιότητες μπορούν να διασωθούν, με το κόστος της εγκατάλειψης των συμμετρικών και διγραμμικών ιδιοτήτων του κλιμακωτού γινομένου, με τον εναλλακτικό ορισμό

a ⋅ b = ∑ a i b i ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

όπου b_i είναι ο μιγαδικός συζυγής του b_i . Τότε το κλιμακωτό γινόμενο οποιουδήποτε διανύσματος με τον εαυτό του είναι ένας μη αρνητικός πραγματικός αριθμός και είναι μη μηδενικό εκτός από το μηδενικό διάνυσμα. Ωστόσο, αυτό το κλιμακωτό γινόμενο δεν είναι γραμμικό ως προς το b (αλλά μάλλον συζυγές γραμμικό), και το κλιμακωτό γινόμενο δεν είναι ούτε συμμετρικό, αφού

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} .

Αυτός ο τύπος του κλιμακωτού γινομένου είναι ωστόσο αρκετά χρήσιμος και οδηγεί στις έννοιες της Ερμιτιανής μορφής και των γενικών εσωτερικών γινόμενων χώρων.

Το εσωτερικό γινόμενο Frobenius γενικεύει το γινόμενο τελείας σε πίνακες. Ορίζεται ως το άθροισμα των γινομένων των αντίστοιχων συνιστωσών δύο πινάκων που έχουν το ίδιο μέγεθος.

Γενίκευση σε τανυστές

Το τετραγωνικό γινόμενο μεταξύ ενός τανυστή τάξης n και ενός τανυστή τάξης m είναι ένας τανυστής τάξης n+m-2. Το τετραγωνικό γινόμενο υπολογίζεται με πολλαπλασιασμό και άθροισμα σε έναν μόνο δείκτη και στους δύο τανυστές. Αν A {\displaystyle \mathbf {A} } και B {\displaystyle \mathbf {B} } είναι δύο τανυστές με αναπαράσταση στοιχείων A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} και B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}}} τα στοιχεία του dot product A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } δίνονται από

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}

Αυτός ο ορισμός ανάγεται φυσικά στο τυπικό διανυσματικό τετραγωνικό γινόμενο όταν εφαρμόζεται σε διανύσματα και στον πολλαπλασιασμό πινάκων όταν εφαρμόζεται σε πίνακες.

Περιστασιακά, ένα διπλό γινόμενο τελείας χρησιμοποιείται για να αναπαραστήσει τον πολλαπλασιασμό και το άθροισμα σε δύο δείκτες. Το διπλό γινόμενο τελείας μεταξύ δύο τανυστών 2ης τάξης είναι ένα κλιμάκιο.

Σχετικές σελίδες

• Ανισότητα Cauchy-Schwarz
• Διασταυρούμενο προϊόν
• Πολλαπλασιασμός πινάκων
• Φυσική