Surface integral

Επιφανειακά ολοκληρώματα κλιμακωτών πεδίων

Θεωρήστε μια επιφάνεια S στην οποία ορίζεται ένα κλιμακωτό πεδίο f. Αν θεωρήσουμε ότι η S είναι φτιαγμένη από κάποιο υλικό και για κάθε x στην S ο αριθμός f(x) είναι η πυκνότητα του υλικού στο x, τότε το επιφανειακό ολοκλήρωμα της f πάνω στην S είναι η μάζα ανά μονάδα πάχους της S. (Αυτό ισχύει μόνο αν η επιφάνεια είναι ένα απειροελάχιστα λεπτό κέλυφος.) Μια προσέγγιση για τον υπολογισμό του επιφανειακού ολοκληρώματος είναι τότε να χωρίσουμε την επιφάνεια σε πολλά πολύ μικρά κομμάτια, να υποθέσουμε ότι σε κάθε κομμάτι η πυκνότητα είναι περίπου σταθερή, να βρούμε τη μάζα ανά μονάδα πάχους κάθε κομματιού πολλαπλασιάζοντας την πυκνότητα του κομματιού επί το εμβαδόν του και στη συνέχεια να αθροίσουμε τους αριθμούς που προκύπτουν για να βρούμε τη συνολική μάζα ανά μονάδα πάχους του S.

Για να βρουν έναν ρητό τύπο για το επιφανειακό ολοκλήρωμα, οι μαθηματικοί παραμετροποιούν το S θεωρώντας στο S ένα σύστημα καμπυλόγραμμων συντεταγμένων, όπως το γεωγραφικό πλάτος και μήκος σε μια σφαίρα. Έστω μια τέτοια παραμετροποίηση x(s, t), όπου το (s, t) μεταβάλλεται σε κάποια περιοχή T στο επίπεδο. Τότε, το επιφανειακό ολοκλήρωμα δίνεται από τη σχέση

∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {\displaystyle \int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right|ds\,dt}

όπου η έκφραση μεταξύ των ράβδων στη δεξιά πλευρά είναι το μέγεθος του διασταυρούμενου γινομένου των μερικών παραγώγων του x(s, t).

Για παράδειγμα, για να βρούμε την επιφάνεια κάποιου γενικού λειτουργικού σχήματος, ας πούμε z = f ( x , y ) {\displaystyle z=f\,(x,y)} , έχουμε

A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\times {\partial \mathbf {r} \over \partial y}\right\|dx\,dy}

όπου r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))} . Άρα ∂ r ∂ x = ( 1 , 0 , f x ( x , y ) ) {\displaystyle {\partial \mathbf {r} \over \partial x}=(1,0,f_{x}(x,y))} , και ∂ r ∂ y = ( 0 , 1 , f y ( x , y ) ) {\displaystyle {\partial \mathbf {r} \over \partial y}=(0,1,f_{y}(x,y))} . Οπότε,

A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}}\,\,dx\,dy\end{aligned}}}

ο οποίος είναι ο τύπος που χρησιμοποιείται για την επιφάνεια ενός γενικού λειτουργικού σχήματος. Μπορεί κανείς να αναγνωρίσει το διάνυσμα στη δεύτερη γραμμή παραπάνω ως το κανονικό διάνυσμα στην επιφάνεια.

Σημειώστε ότι λόγω της παρουσίας του διασταυρούμενου γινομένου, οι παραπάνω τύποι λειτουργούν μόνο για επιφάνειες ενσωματωμένες σε τρισδιάστατο χώρο.

Επιφανειακά ολοκληρώματα διανυσματικών πεδίων

Θεωρήστε ένα διανυσματικό πεδίο v στο S, δηλαδή για κάθε x στο S, το v(x) είναι ένα διάνυσμα.

Το επιφανειακό ολοκλήρωμα μπορεί να οριστεί κατά συνιστώσες σύμφωνα με τον ορισμό του επιφανειακού ολοκληρώματος ενός κλιμακωτού πεδίου- το αποτέλεσμα είναι ένα διάνυσμα. Για παράδειγμα, αυτό ισχύει για το ηλεκτρικό πεδίο σε κάποιο σταθερό σημείο που οφείλεται σε μια ηλεκτρικά φορτισμένη επιφάνεια ή για τη βαρύτητα σε κάποιο σταθερό σημείο που οφείλεται σε ένα φύλλο υλικού. Μπορεί επίσης να υπολογίσει τη μαγνητική ροή μέσω μιας επιφάνειας.

Εναλλακτικά, οι μαθηματικοί μπορούν να ολοκληρώσουν την κανονική συνιστώσα του διανυσματικού πεδίου- το αποτέλεσμα είναι ένα κλιμάκιο. Ένα παράδειγμα είναι ένα ρευστό που ρέει μέσα από το S, έτσι ώστε το v(x) καθορίζει την ταχύτητα του ρευστού στο x. Η ροή ορίζεται ως η ποσότητα του ρευστού που ρέει μέσα από το S σε μια μονάδα χρόνου.

Αυτή η απεικόνιση υποδηλώνει ότι αν το διανυσματικό πεδίο εφάπτεται στο S σε κάθε σημείο, τότε η ροή είναι μηδενική, επειδή το ρευστό ρέει απλώς παράλληλα στο S και ούτε μέσα ούτε έξω. Αυτό συνεπάγεται επίσης ότι αν το v δεν ρέει μόνο κατά μήκος του S, δηλαδή αν το v έχει και εφαπτομενική και κανονική συνιστώσα, τότε μόνο η κανονική συνιστώσα συμβάλλει στη ροή. Με βάση αυτό το συλλογισμό, για να βρούμε τη ροή, πρέπει να πάρουμε το τετραγωνικό γινόμενο του v με τη μοναδιαία επιφανειακή κάθετη στο S σε κάθε σημείο, το οποίο θα μας δώσει ένα κλιμακωτό πεδίο, και να ολοκληρώσουμε το λαμβανόμενο πεδίο όπως παραπάνω. Αυτό δίνει τον τύπο

∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . {\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right)ds\,dt. }

Το διασταυρούμενο γινόμενο στη δεξιά πλευρά αυτής της έκφρασης είναι μια επιφανειακή κανονική που καθορίζεται από την παραμετροποίηση.

Αυτός ο τύπος ορίζει το ολοκλήρωμα στα αριστερά (προσέξτε την τελεία και τον διανυσματικό συμβολισμό για το στοιχείο της επιφάνειας).

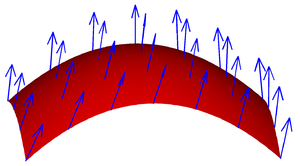
Ένα διανυσματικό πεδίο σε μια επιφάνεια.

Θεωρήματα που αφορούν επιφανειακά ολοκληρώματα

Διάφορα χρήσιμα αποτελέσματα για επιφανειακά ολοκληρώματα μπορούν να προκύψουν χρησιμοποιώντας τη διαφορική γεωμετρία και το διανυσματικό λογισμό, όπως το θεώρημα της απόκλισης και η γενίκευσή του, το θεώρημα του Stokes.

Προχωρημένα ζητήματα

Αλλαγή παραμετροποίησης

Η παραπάνω συζήτηση όρισε το επιφανειακό ολοκλήρωμα χρησιμοποιώντας μια παραμετροποίηση της επιφάνειας S. Μια δεδομένη επιφάνεια μπορεί να έχει πολλές παραμετροποιήσεις. Για παράδειγμα, όταν οι θέσεις του Βόρειου και του Νότιου Πόλου μετακινούνται σε μια σφαίρα, το γεωγραφικό πλάτος και το γεωγραφικό μήκος αλλάζουν για όλα τα σημεία της σφαίρας. Ένα φυσικό ερώτημα είναι τότε αν ο ορισμός του επιφανειακού ολοκληρώματος εξαρτάται από την επιλεγμένη παραμετροποίηση. Για ολοκληρώματα κλιμακωτών πεδίων, η απάντηση σε αυτό το ερώτημα είναι απλή, η τιμή του επιφανειακού ολοκληρώματος θα είναι η ίδια ανεξάρτητα από την παραμετροποίηση που θα χρησιμοποιηθεί.

Τα ολοκληρώματα διανυσματικών πεδίων είναι πιο περίπλοκα, επειδή εμπλέκεται η κανονική της επιφάνειας. Οι μαθηματικοί έχουν αποδείξει ότι δεδομένης δύο παραμετροποιήσεων της ίδιας επιφάνειας, των οποίων οι επιφανειακές κανονικές δείχνουν προς την ίδια κατεύθυνση, και οι δύο παραμετροποιήσεις δίνουν την ίδια τιμή για το επιφανειακό ολοκλήρωμα. Εάν, ωστόσο, οι κανονικές αυτών των παραμετροποιήσεων δείχνουν σε αντίθετες κατευθύνσεις, η τιμή του επιφανειακού ολοκληρώματος που λαμβάνεται με τη μία παραμετροποίηση είναι η αρνητική της τιμής που λαμβάνεται μέσω της άλλης παραμετροποίησης. Προκύπτει ότι δεδομένης μιας επιφάνειας, δεν χρειάζεται να επιμείνουμε σε κάποια μοναδική παραμετροποίηση- αλλά, όταν ολοκληρώνουμε διανυσματικά πεδία, πρέπει να αποφασίσουμε εκ των προτέρων προς ποια κατεύθυνση θα δείχνει η κανονική και στη συνέχεια να επιλέξουμε οποιαδήποτε παραμετροποίηση που να είναι σύμφωνη με αυτή την κατεύθυνση.

Οι παραμετροποιήσεις λειτουργούν σε τμήματα της επιφάνειας

Ένα άλλο ζήτημα είναι ότι μερικές φορές οι επιφάνειες δεν έχουν παραμετροποιήσεις που να καλύπτουν ολόκληρη την επιφάνεια- αυτό ισχύει για παράδειγμα για την επιφάνεια ενός κυλίνδρου (πεπερασμένου ύψους). Η προφανής λύση είναι τότε να χωρίσετε την επιφάνεια αυτή σε διάφορα κομμάτια, να υπολογίσετε το επιφανειακό ολοκλήρωμα σε κάθε κομμάτι και στη συνέχεια να τα προσθέσετε όλα μαζί. Πράγματι έτσι λειτουργούν τα πράγματα, αλλά όταν ολοκληρώνει κανείς διανυσματικά πεδία πρέπει και πάλι να προσέχει πώς θα επιλέξει το διάνυσμα κανονικού σημείου για κάθε κομμάτι της επιφάνειας, έτσι ώστε όταν τα κομμάτια συναρμολογηθούν, τα αποτελέσματα να είναι συνεπή. Για τον κύλινδρο, αυτό σημαίνει ότι αν αποφασίσουμε ότι για την πλαϊνή περιοχή η κανονική θα δείχνει έξω από το σώμα, τότε για τα πάνω και κάτω κυκλικά τμήματα η κανονική πρέπει να δείχνει επίσης έξω από το σώμα.

Ασυνεπείς κανονικές επιφάνειας

Τέλος, υπάρχουν επιφάνειες που δεν έχουν μια επιφανειακή κανονική σε κάθε σημείο με συνεπή αποτελέσματα (για παράδειγμα, η λωρίδα Möbius). Εάν μια τέτοια επιφάνεια χωριστεί σε κομμάτια, σε κάθε κομμάτι επιλεγεί μια παραμετροποίηση και η αντίστοιχη επιφανειακή κανονική και τα κομμάτια συναρμολογηθούν, τα κανονικά διανύσματα που προέρχονται από διαφορετικά κομμάτια δεν μπορούν να συμβιβαστούν. Αυτό σημαίνει ότι σε κάποια διασταύρωση μεταξύ δύο κομματιών θα υπάρχουν κανονικά διανύσματα που θα δείχνουν προς αντίθετες κατευθύνσεις. Μια τέτοια επιφάνεια ονομάζεται μη προσανατολισμένη. Τα διανυσματικά πεδία δεν μπορούν να ολοκληρωθούν σε μη προσανατολισμένες επιφάνειες.

Σχετικές σελίδες

• Θεώρημα απόκλισης
• Θεώρημα του Stokes
• Γραμμικό ολοκλήρωμα
• Ολοκληρωμένος όγκος
• Καρτεσιανό σύστημα συντεταγμένων
• Στοιχεία όγκου και επιφάνειας σε σφαιρικό σύστημα συντεταγμένων
• Στοιχεία όγκου και επιφάνειας σε κυλινδρικό σύστημα συντεταγμένων
• Μέθοδος Holstein-Herring