Αρμονική σειρά (Μαθηματικά)

Στα μαθηματικά, η αρμονική σειρά είναι η αποκλίνουσα άπειρη σειρά:

∑ n = 1 ∞ 1 n = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } $\sum _{n=1}^{\infty }{\frac {1}{n}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Αποκλίνουσα σημαίνει ότι καθώς προσθέτετε περισσότερους όρους, το άθροισμα δεν σταματά ποτέ να γίνεται μεγαλύτερο. Δεν κατευθύνεται προς μια ενιαία πεπερασμένη τιμή.

Άπειρος σημαίνει ότι μπορείτε πάντα να προσθέσετε έναν ακόμη όρο. Δεν υπάρχει τελικός όρος στη σειρά.

Το όνομά της προέρχεται από την ιδέα των αρμονικών στη μουσική: τα μήκη κύματος των υπερτονίων μιας δονούμενης χορδής είναι το 1/2, 1/3, 1/4, κ.λπ. του θεμελιώδους μήκους κύματος της χορδής. Εκτός από τον πρώτο όρο, κάθε όρος της σειράς είναι ο αρμονικός μέσος όρος των όρων εκατέρωθεν αυτού. Η φράση αρμονικός μέσος προέρχεται επίσης από τη μουσική.

Ιστορία

Το γεγονός ότι η αρμονική σειρά αποκλίνει αποδείχθηκε για πρώτη φορά τον 14ο αιώνα από τον Nicole Oresme, αλλά ξεχάστηκε. Αποδείξεις δόθηκαν τον 17ο αιώνα από τους Pietro Mengoli, Johann Bernoulli και Jacob Bernoulli.

Οι αρμονικές ακολουθίες έχουν χρησιμοποιηθεί από αρχιτέκτονες. Κατά την περίοδο του Μπαρόκ οι αρχιτέκτονες τις χρησιμοποίησαν στις αναλογίες των κατόψεων, των όψεων και στις σχέσεις μεταξύ των αρχιτεκτονικών λεπτομερειών των εκκλησιών και των παλατιών.

Απόκλιση

Υπάρχουν αρκετές γνωστές αποδείξεις για την απόκλιση της αρμονικής σειράς. Μερικές από αυτές παρατίθενται παρακάτω.

Δοκιμή σύγκρισης

Ένας τρόπος απόδειξης της απόκλισης είναι η σύγκριση της αρμονικής σειράς με μια άλλη αποκλίνουσα σειρά, όπου κάθε παρονομαστής αντικαθίσταται με την αμέσως μεγαλύτερη δύναμη του δύο:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}}+{\frac {1}{8}}}+{\frac {1}{9}}+\cdots \\\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16}} }}}+\cdots \end{aligned}}}} ${\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{\color {red}{\mathbf {8} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16} }}}+\cdots \end{aligned}}$

Κάθε όρος της αρμονικής σειράς είναι μεγαλύτερος ή ίσος με τον αντίστοιχο όρο της δεύτερης σειράς και, επομένως, το άθροισμα της αρμονικής σειράς πρέπει να είναι μεγαλύτερο ή ίσο με το άθροισμα της δεύτερης σειράς. Ωστόσο, το άθροισμα της δεύτερης σειράς είναι άπειρο:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}} ${\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}\right)+\left({\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\right)+\left({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\right)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}$

Προκύπτει (με το τεστ σύγκρισης) ότι το άθροισμα των αρμονικών σειρών πρέπει επίσης να είναι άπειρο. Πιο συγκεκριμένα, η παραπάνω σύγκριση αποδεικνύει ότι

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}} $\sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}$

για κάθε θετικό ακέραιο $k$ .

Η απόδειξη αυτή, που προτάθηκε από τη Nicole Oresme γύρω στο 1350, θεωρείται κορυφαία των μεσαιωνικών μαθηματικών. Αποτελεί ακόμη και σήμερα μια τυπική απόδειξη που διδάσκεται στα μαθήματα μαθηματικών.

Ολοκληρωμένη δοκιμή

Είναι δυνατόν να αποδειχθεί ότι η αρμονική σειρά αποκλίνει συγκρίνοντας το άθροισμά της με ένα ακατάλληλο ολοκλήρωμα. Σκεφτείτε τη διάταξη των ορθογωνίων που φαίνεται στο σχήμα στα δεξιά. Κάθε ορθογώνιο έχει πλάτος 1 μονάδα και ύψος 1/n μονάδες, οπότε το συνολικό εμβαδόν του άπειρου αριθμού ορθογωνίων είναι το άθροισμα της αρμονικής σειράς:

εμβαδόν ορθογωνίων = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{area of}}\\\{\text{rectangles}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots } ${\begin{array}{c}{\text{area of}}\\{\text{rectangles}}\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}+\cdots$

Το συνολικό εμβαδόν κάτω από την καμπύλη $y =$ 1/x από το 1 έως το άπειρο δίνεται από ένα αποκλίνον ακατάλληλο ολοκλήρωμα:

περιοχή κάτω από την καμπύλη = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{area under}}\\\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty . } ${\begin{array}{c}{\text{area under}}\\{\text{curve}}\end{array}}=\int _{1}^{\infty }{\frac {1}{x}}\,dx=\infty .$

Εφόσον το εμβαδόν αυτό περιέχεται εξ ολοκλήρου στα ορθογώνια, το συνολικό εμβαδόν των ορθογωνίων πρέπει να είναι επίσης άπειρο. Αυτό αποδεικνύει ότι

∑ n = 1 k 1 n > ∫ 1 k + 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1). } $\sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1).$

Η γενίκευση αυτού του επιχειρήματος είναι γνωστή ως δοκιμή ολοκλήρωσης.

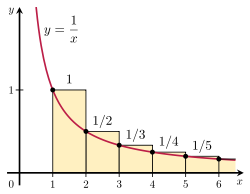
Απεικόνιση της ολοκληρωτικής δοκιμής.

Ρυθμός απόκλισης

Η αρμονική σειρά αποκλίνει πολύ αργά. Για παράδειγμα, το άθροισμα των πρώτων 1043 όρων είναι μικρότερο από 100. Αυτό οφείλεται στο γεγονός ότι τα επιμέρους αθροίσματα της σειράς έχουν λογαριθμική ανάπτυξη. Συγκεκριμένα,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1} $\sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gamma +\varepsilon _{k}\leq (\ln k)+1$

όπου $γ$ είναι η σταθερά Euler-Mascheroni και $εk ~$ 1/2k που πλησιάζει το 0 καθώς $το k$ πηγαίνει στο άπειρο. Ο Leonhard Euler απέδειξε τόσο αυτό όσο και ότι το άθροισμα που περιλαμβάνει μόνο τα αντίστροφα των πρώτων αριθμών αποκλίνει επίσης, δηλαδή:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}}+{\frac {1}{7}}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty . } $\sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty .$

Μερικά αθροίσματα

Οι τριάντα πρώτοι αρμονικοί αριθμοί
$n$	Μερικό άθροισμα της αρμονικής σειράς, $Hn$
$n$	εκφρασμένο ως κλάσμα		δεκαδικό	σχετικό μέγεθος
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Τα πεπερασμένα μερικά αθροίσματα των αποκλινουσών αρμονικών σειρών,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},} $H_{n}=\sum _{k=1}^{n}{\frac {1}{k}},$

ονομάζονται αρμονικοί αριθμοί.

Η διαφορά μεταξύ $Hn$ και $ln n$ συγκλίνει στη σταθερά Euler-Mascheroni. Η διαφορά μεταξύ δύο οποιωνδήποτε αρμονικών αριθμών δεν είναι ποτέ ακέραιος αριθμός. Κανένας αρμονικός αριθμός δεν είναι ακέραιος, εκτός από τον $H1 = 1$ .

Σχετικές σειρές

Εναλλασσόμενη αρμονική σειρά

Η σειρά

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots } $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots$

είναι γνωστή ως εναλλασσόμενη αρμονική σειρά. Η σειρά αυτή συγκλίνει με τη δοκιμή εναλλασσόμενης σειράς. Συγκεκριμένα, το άθροισμα είναι ίσο με τον φυσικό λογάριθμο του 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.} $1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.$

Η εναλλασσόμενη αρμονική σειρά, αν και υπό όρους συγκλίνουσα, δεν είναι απολύτως συγκλίνουσα: αν οι όροι της σειράς αναδιαταχθούν συστηματικά, γενικά το άθροισμα γίνεται διαφορετικό και, ανάλογα με την αναδιάταξη, ενδεχομένως ακόμη και άπειρο.

Ο τύπος της εναλλασσόμενης αρμονικής σειράς είναι μια ειδική περίπτωση της σειράς Mercator, της σειράς Taylor για τον φυσικό λογάριθμο.

Μια σχετική σειρά μπορεί να προκύψει από τη σειρά Taylor για τον ορθογώνιο:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}. } $\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}.$

Αυτό είναι γνωστό ως σειρά Leibniz.

Γενική αρμονική σειρά

Η γενική αρμονική σειρά έχει τη μορφή

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},} $\sum _{n=0}^{\infty }{\frac {1}{an+b}},$

όπου $a \neq 0$ και $b$ είναι πραγματικοί αριθμοί και το b/a δεν είναι μηδέν ή αρνητικός ακέραιος $.$

Με τη δοκιμή σύγκρισης ορίων με τις αρμονικές σειρές, όλες οι γενικές αρμονικές σειρές αποκλίνουν επίσης.

$σειρά p$

Μια γενίκευση της αρμονικής σειράς είναι η $σειρά p$ (ή υπεραρμονική σειρά), η οποία ορίζεται ως εξής

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}} $\sum _{n=1}^{\infty }{\frac {1}{n^{p}}}$

για κάθε πραγματικό αριθμό $p$ . Όταν $p = 1$ , η $σειρά p$ είναι η αρμονική σειρά, η οποία αποκλίνει $.$ Είτε το τεστ ολοκλήρωσης είτε το τεστ συμπύκνωσης Cauchy δείχνει ότι η $σειρά p$ συγκλίνει για όλα τα $p > 1 ($ οπότε ονομάζεται υπερ-αρμονική σειρά) και αποκλίνει για όλα τα p $\leq 1.$ Εάν $p > 1$ τότε το άθροισμα της σειράς p είναι ζ( $p), δηλαδή$ η συνάρτηση ζ του Riemann που αξιολογείται στο p $.$

Το πρόβλημα της εύρεσης του αθροίσματος για $p = 2$ ονομάζεται πρόβλημα της Βασιλείας- ο Leonhard Euler έδειξε ότι είναι $π2/6$ . Η τιμή του αθροίσματος για $p = 3$ ονομάζεται σταθερά του Apéry, καθώς ο Roger Apéry απέδειξε ότι είναι ένας άρρητος αριθμός.

σειρά ln

Σχετική με τη $σειρά p$ είναι η σειρά ln, η οποία ορίζεται ως εξής

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}} $\sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}$

για κάθε θετικό πραγματικό αριθμό $p$ . Αυτό μπορεί να αποδειχθεί με το τεστ ολοκλήρωσης ότι αποκλίνει για $p \leq 1$ αλλά συγκλίνει για όλα τα $p > 1.$

$σειρά φ$

Για κάθε κυρτή συνάρτηση πραγματικής αξίας $φ$ , τέτοια ώστε

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2, {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}}\right)}{\varphi (u)}}<{\frac {1}{2}}},} $\limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}\right)}{\varphi (u)}}<{\frac {1}{2}},$

η σειρά

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)} $\sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}\right)$

είναι συγκλίνουσα. ^[]

Τυχαία αρμονική σειρά

Η τυχαία αρμονική σειρά

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},} $\sum _{n=1}^{\infty }{\frac {s_{n}}{n}},$

όπου οι $sn$ είναι ανεξάρτητες, πανομοιότυπα κατανεμημένες τυχαίες μεταβλητές που παίρνουν τις τιμές +1 και -1 με ίση πιθανότητα 1/2, είναι ένα γνωστό παράδειγμα στη θεωρία πιθανοτήτων για μια σειρά τυχαίων μεταβλητών που συγκλίνει με πιθανότητα 1. Το γεγονός αυτής της σύγκλισης είναι μια εύκολη συνέπεια είτε του θεωρήματος των τριών σειρών Kolmogorov είτε της στενά σχετιζόμενης μέγιστης ανισότητας Kolmogorov. Ο Byron Schmuland του Πανεπιστημίου της Αλμπέρτα εξέτασε περαιτέρω τις ιδιότητες της τυχαίας αρμονικής σειράς και έδειξε ότι η συγκλίνουσα σειρά είναι μια τυχαία μεταβλητή με ορισμένες ενδιαφέρουσες ιδιότητες. Συγκεκριμένα, η συνάρτηση πυκνότητας πιθανότητας αυτής της τυχαίας μεταβλητής που εκτιμάται στο +2 ή στο -2 παίρνει την τιμή 0,1249999999999999999999999999999999999999999999999999764..., διαφέροντας από το 1/8 κατά λιγότερο από 10-42. Η εργασία του Schmuland εξηγεί γιατί αυτή η πιθανότητα είναι τόσο κοντά, αλλά όχι ακριβώς, στο 1/8. Η ακριβής τιμή αυτής της πιθανότητας δίνεται από το άπειρο ολοκλήρωμα του συνημιτονοειδούς γινομένου $C2$ διαιρεμένο με το $π$ .

Εξαντλημένη αρμονική σειρά

Η εξαντλημένη αρμονική σειρά όπου αφαιρούνται όλοι οι όροι στους οποίους το ψηφίο 9 εμφανίζεται οπουδήποτε στον παρονομαστή μπορεί να αποδειχθεί ότι συγκλίνει και η τιμή της είναι μικρότερη από 80. Στην πραγματικότητα, όταν αφαιρούνται όλοι οι όροι που περιέχουν οποιαδήποτε συγκεκριμένη σειρά ψηφίων (σε οποιαδήποτε βάση), η σειρά συγκλίνει.

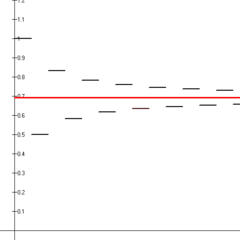
Τα δεκατέσσερα πρώτα μερικά αθροίσματα της εναλλασσόμενης αρμονικής σειράς (μαύρα τμήματα γραμμής) που παρουσιάζονται να συγκλίνουν στον φυσικό λογάριθμο του 2 (κόκκινη γραμμή).

Εφαρμογές

Η αρμονική σειρά μπορεί να είναι αντιφατική. Αυτό οφείλεται στο γεγονός ότι είναι μια αποκλίνουσα σειρά, παρόλο που οι όροι της σειράς γίνονται μικρότεροι και βαίνουν προς το μηδέν. Η απόκλιση της αρμονικής σειράς είναι η πηγή ορισμένων παραδόξων.

Το "σκουλήκι στο λαστιχάκι". Ας υποθέσουμε ότι ένα σκουλήκι σέρνεται κατά μήκος μιας απείρως ελαστικής λαστιχένιας ταινίας μήκους ενός μέτρου την ίδια στιγμή που η λαστιχένια ταινία τεντώνεται ομοιόμορφα. Αν το σκουλήκι ταξιδεύει 1 εκατοστό ανά λεπτό και η ταινία τεντώνεται 1 μέτρο ανά λεπτό, θα φτάσει ποτέ το σκουλήκι στο τέλος της ελαστικής ταινίας; Η απάντηση, αντιφατικά, είναι "ναι", διότι μετά από $n$ λεπτά, ο λόγος της απόστασης που διανύει το σκουλήκι προς το συνολικό μήκος της ελαστικής ταινίας είναι

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}. } ${\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Επειδή η σειρά γίνεται αυθαίρετα μεγάλη καθώς $το n$ μεγαλώνει, τελικά ο λόγος αυτός πρέπει να υπερβεί το 1, πράγμα που σημαίνει ότι το σκουλήκι φτάνει στο τέλος της λαστιχένιας ταινίας. Ωστόσο, η τιμή του $n$ στην οποία συμβαίνει αυτό πρέπει να είναι εξαιρετικά μεγάλη: περίπου e100, ένας αριθμός που υπερβαίνει τα 1043 λεπτά (1037 χρόνια). Αν και η αρμονική σειρά αποκλίνει, το κάνει πολύ αργά.

Το πρόβλημα του Jeep ρωτάει πόσα συνολικά καύσιμα απαιτούνται για ένα αυτοκίνητο με περιορισμένη χωρητικότητα μεταφοράς καυσίμων για να διασχίσει μια έρημο αφήνοντας σταγόνες καυσίμων κατά μήκος της διαδρομής. Η απόσταση που μπορεί να διανύσει το αυτοκίνητο με δεδομένη ποσότητα καυσίμου σχετίζεται με τα επιμέρους αθροίσματα της αρμονικής σειράς, τα οποία αυξάνονται λογαριθμικά. Και έτσι τα απαιτούμενα καύσιμα αυξάνονται εκθετικά με την επιθυμητή απόσταση.

Το πρόβλημα της στοίβαξης με τουβλάκια: με δεδομένη μια συλλογή πανομοιότυπων ντόμινο, είναι δυνατόν να τα στοιβάξετε στην άκρη ενός τραπεζιού έτσι ώστε να κρέμονται πάνω από την άκρη του τραπεζιού χωρίς να πέφτουν. Το αντιφατικό αποτέλεσμα είναι ότι μπορούν να στοιβαχτούν με τρόπο που να κάνει την προεξοχή όσο μεγάλη θέλετε. Δηλαδή, εφόσον υπάρχουν αρκετά ντόμινο.

Ένας κολυμβητής που πηγαίνει πιο γρήγορα κάθε φορά που αγγίζει τον τοίχο της πισίνας. Ο κολυμβητής αρχίζει να διασχίζει μια πισίνα 10 μέτρων με ταχύτητα 2 m/s και με κάθε διάσχιση προστίθενται άλλα 2 m/s στην ταχύτητά του. Θεωρητικά, η ταχύτητα του κολυμβητή είναι απεριόριστη, αλλά ο αριθμός των διασχίσεων της πισίνας που απαιτούνται για να επιτευχθεί αυτή η ταχύτητα γίνεται πολύ μεγάλος- για παράδειγμα, για να φτάσει στην ταχύτητα του φωτός (αγνοώντας την ειδική σχετικότητα), ο κολυμβητής πρέπει να διασχίσει την πισίνα 150 εκατομμύρια φορές. Σε αντίθεση με αυτόν τον μεγάλο αριθμό, ο χρόνος που απαιτείται για να επιτευχθεί μια δεδομένη ταχύτητα εξαρτάται από το άθροισμα των σειρών σε κάθε δεδομένο αριθμό διαβάσεων της πισίνας:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}. } ${\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}.$

Ο υπολογισμός του αθροίσματος δείχνει ότι ο χρόνος που απαιτείται για να φτάσουμε στην ταχύτητα του φωτός είναι μόνο 97 δευτερόλεπτα.

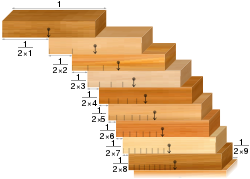
Το πρόβλημα της στοίβαξης μπλοκ: μπλοκ ευθυγραμμισμένα σύμφωνα με την αρμονική σειρά γεφυρώνουν σχισμές οποιουδήποτε πλάτους.

Σχετικές σελίδες

Αρμονική εξέλιξη
Κατάλογος των αθροισμάτων των αμοιβαίων

Ερωτήσεις και απαντήσεις

Q: Τι είναι η αρμονική σειρά;

A: Η αρμονική σειρά είναι μια άπειρη αποκλίνουσα σειρά όπου κάθε όρος ισούται με 1 διαιρεμένο με τη θέση του στην ακολουθία.

Ερ: Τι σημαίνει ότι μια σειρά είναι αποκλίνουσα;

Α: Αποκλίνουσα σημαίνει ότι καθώς προσθέτετε περισσότερους όρους, το άθροισμα δεν σταματά ποτέ να μεγαλώνει και δεν κατευθύνεται προς μια ενιαία πεπερασμένη τιμή.

Ερ: Τι σημαίνει ότι μια σειρά είναι άπειρη;

Α: Άπειρο σημαίνει ότι μπορείτε πάντα να προσθέσετε έναν ακόμη όρο και ότι δεν υπάρχει τελικός όρος στη σειρά.

Ερ: Από πού προήλθε το όνομα αυτής της σειράς;

Α: Το όνομα αυτής της σειράς προέρχεται από την ιδέα των αρμονικών στη μουσική, όπου τα μήκη κύματος των υπέρτονων είναι το 1/2, 1/3, 1/4 κ.λπ. του θεμελιώδους μήκους κύματος της χορδής.

Ε: Τι σημαίνει αρμονική;

A: Αρμονικός μέσος όρος είναι όταν κάθε όρος σε μια ακολουθία είναι ίσος με τον αρμονικό μέσο όρο των γειτονικών του όρων. Αυτή η φράση προέρχεται επίσης από τη μουσική.

Ερ: Πώς υπολογίζουμε κάθε όρο αυτής της ακολουθίας;

Α: Κάθε όρος σε αυτή την ακολουθία μπορεί να υπολογιστεί διαιρώντας το ένα με τη θέση του στην ακολουθία (1/n).